Question
Question: A horizontal cylindrical pipe consists of two coaxial sections, the section to the left has cross-se...
A horizontal cylindrical pipe consists of two coaxial sections, the section to the left has cross-sectional area A and that to the right has a cross-sectional area 3A. Some amount of water is enclosed in the pipe two airtight pistons. The smaller piston is connected to a fixed support with the help of a spring of force constant k and another spring of force constant 2k is connected with the larger piston as shown in the Figure. If the free end P of the spring connected to the larger piston is slowly shifted by a distance Δx, how much will the other spring be extended?
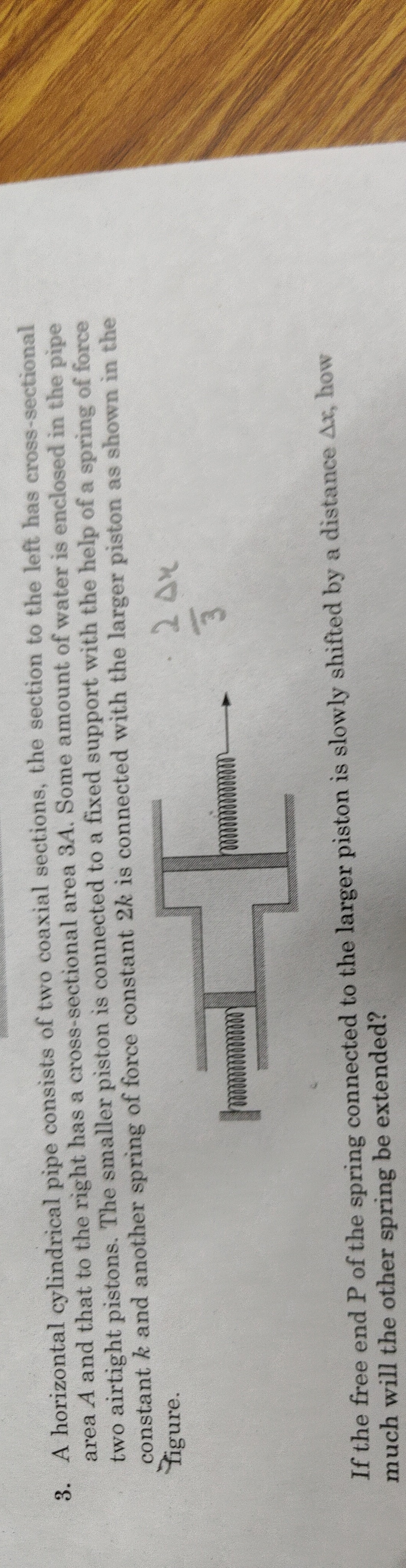
32Δx
23Δx
Δx
31Δx
32Δx
Solution
Let x1 and x2 be the extensions of the springs connected to the smaller piston (area A) and the larger piston (area 3A), respectively. The pressure exerted by the smaller piston is P=Akx1. The pressure exerted by the larger piston is P=3A2kx2. Equating these pressures gives Akx1=3A2kx2, which simplifies to x1=32x2. Therefore, Δx1=32Δx2. Given that the larger piston is shifted by Δx, we have Δx2=Δx. Thus, Δx1=32Δx.
