Question
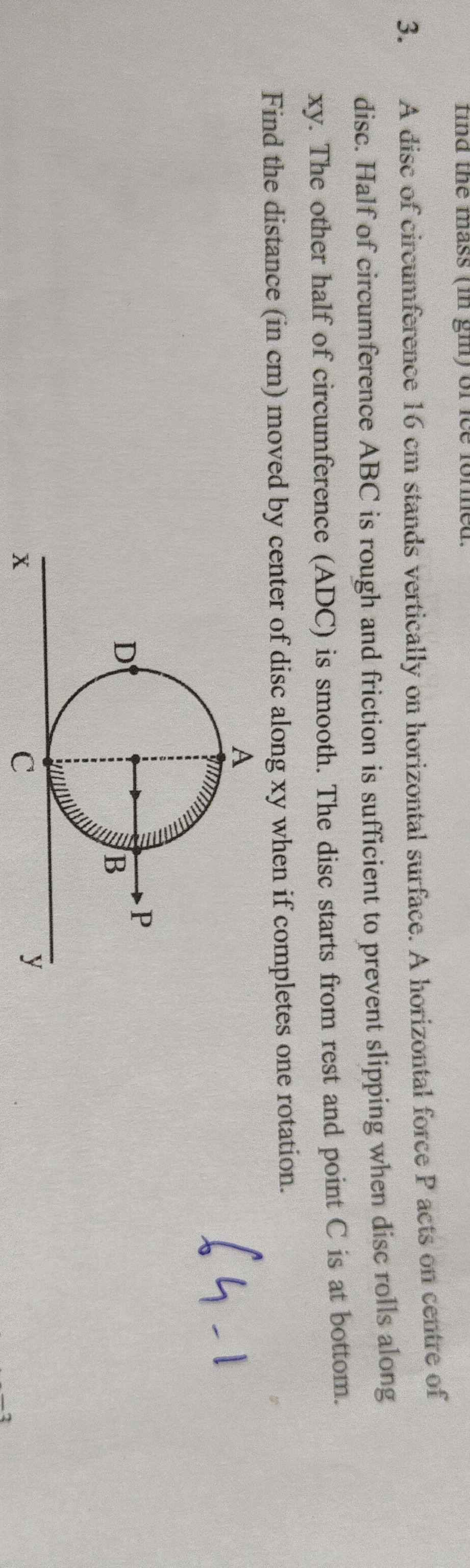
Question: A disc of circumference 16 cm stands vertically on horizontal surface. A horizontal force P acts on ...
A disc of circumference 16 cm stands vertically on horizontal surface. A horizontal force P acts on centre of disc. Half of circumference ABC is rough and friction is sufficient to prevent slipping when disc rolls along xy. The other half of circumference (ADC) is smooth. The disc starts from rest and point C is at bottom. Find the distance (in cm) moved by center of disc along xy when if completes one rotation.
19
Solution
The problem describes a disc rolling on a horizontal surface under the action of a horizontal force P at its center. The circumference of the disc is 16 cm. Half of the circumference (ABC) is rough, allowing for rolling without slipping, while the other half (ADC) is smooth. The disc starts from rest with point C at the bottom and completes one full rotation. We need to find the total distance moved by the center of the disc.
First, let's determine the radius of the disc: Circumference C=2πR=16 cm. So, the radius R=2π16=π8 cm.
The motion can be divided into two phases, each covering half a rotation (π radians):
Phase 1: Rough surface (ABC) in contact with the ground (from C to A at bottom)
-
The disc starts from rest.
-
The surface is rough, and friction is sufficient to prevent slipping. This means the disc rolls without slipping.
-
When a disc rolls without slipping, the distance moved by its center of mass is equal to the arc length of the circumference that has come into contact with the ground.
-
Since this phase covers half a rotation, the angular displacement is Δθ1=π radians.
-
The distance moved by the center of mass in this phase, x1, is given by: x1=RΔθ1=Rπ=(π8)π=8 cm.
-
Let's analyze the dynamics in this phase to find the velocity at the end of this phase.
- Linear equation of motion: P−f=Ma1 (where f is the static friction force, opposing the tendency to slip forward due to P).
- Rotational equation of motion about the center of mass: fR=Iα1. For a disc, I=21MR2. So, fR=21MR2α1⟹f=21MRα1.
- No-slip condition: a1=Rα1. So, f=21Ma1.
- Substitute f into the linear equation: P−21Ma1=Ma1⟹P=23Ma1.
- Therefore, the acceleration of the center of mass in this phase is a1=3M2P.
-
The velocity of the center of mass at the end of Phase 1 (when point A is at the bottom), v1, can be found using kinematics: v12=u2+2a1x1. Since u=0: v12=2a1x1=2(3M2P)(8)=3M32P.
-
The angular velocity at the end of Phase 1 is ω1=Rv1.
Phase 2: Smooth surface (ADC) in contact with the ground (from A to C at bottom)
- This phase also covers half a rotation, so the angular displacement is Δθ2=π radians.
- The surface is smooth, meaning there is no friction (f=0).
- Linear equation of motion: P=Ma2. So, the acceleration of the center of mass is a2=MP.
- Rotational equation of motion about the center of mass: Since there is no friction, there is no torque about the center of mass. Therefore, the angular acceleration α2=0.
- This implies that the angular velocity remains constant throughout Phase 2, i.e., ω2=ω1.
- The time taken for this phase, t2, can be found from the angular displacement: Δθ2=ω1t2⟹π=ω1t2. Since ω1=v1/R, we have t2=ω1π=v1πR.
- The distance moved by the center of mass in Phase 2, x2, can be found using kinematics: x2=v1t2+21a2t22. Substitute t2=v1πR and a2=MP: x2=v1(v1πR)+21(MP)(v1πR)2 x2=πR+21(MP)v12π2R2.
- From Phase 1, we found v12=3M32P. From this, we can express MP: MP=323v12.
- Substitute this expression for MP into the equation for x2: x2=πR+21(323v12)v12π2R2 x2=πR+643π2R2.
- Now substitute the value of R=π8 cm: x2=π(π8)+643π2(π8)2 x2=8+643π2(π264) x2=8+643×64 x2=8+3=11 cm.
Total distance moved by the center of the disc: The total distance moved by the center of the disc when it completes one rotation is the sum of distances from Phase 1 and Phase 2. Xtotal=x1+x2=8 cm+11 cm=19 cm.
Explanation of the solution:
- Calculate Radius: From the given circumference, find the radius R=C/(2π)=16/(2π)=8/π cm.
- Phase 1 (Rough, No Slip): The first half rotation (from C to A) occurs on the rough surface where there's no slipping.
- Distance moved by center of mass x1=R×(angle)=Rπ=(8/π)π=8 cm.
- Using Newton's second law for translation (P−f=Ma1) and rotation (fR=Iα1), along with the no-slip condition (a1=Rα1 and I=MR2/2), find the acceleration a1=2P/(3M).
- Calculate the square of the velocity at the end of Phase 1: v12=2a1x1=2(2P/(3M))(8)=32P/(3M).
- Phase 2 (Smooth, Slipping): The second half rotation (from A to C) occurs on the smooth surface, so friction is zero.
- Linear acceleration a2=P/M (since f=0).
- Angular acceleration α2=0 (since no torque). This means angular velocity ω2=ω1 (constant).
- Time taken for this half rotation t2=angle/ω1=π/ω1=πR/v1.
- Distance moved by center of mass x2=v1t2+(1/2)a2t22.
- Substitute t2 and a2: x2=πR+(1/2)(P/M)(πR/v1)2.
- Substitute P/M=3v12/32 (derived from v12 expression in Phase 1): x2=πR+(1/2)(3v12/32)(π2R2/v12)=πR+3π2R2/64.
- Substitute R=8/π: x2=π(8/π)+3π2(8/π)2/64=8+3π2(64/π2)/64=8+3=11 cm.
- Total Distance: Sum the distances from both phases: Xtotal=x1+x2=8+11=19 cm.
Subject: Physics Chapter: Rotational Motion (or System of Particles and Rotational Motion) Topic: Rolling Motion (or Combined Translation and Rotation) Difficulty Level: Medium Question Type: Integer
