Question

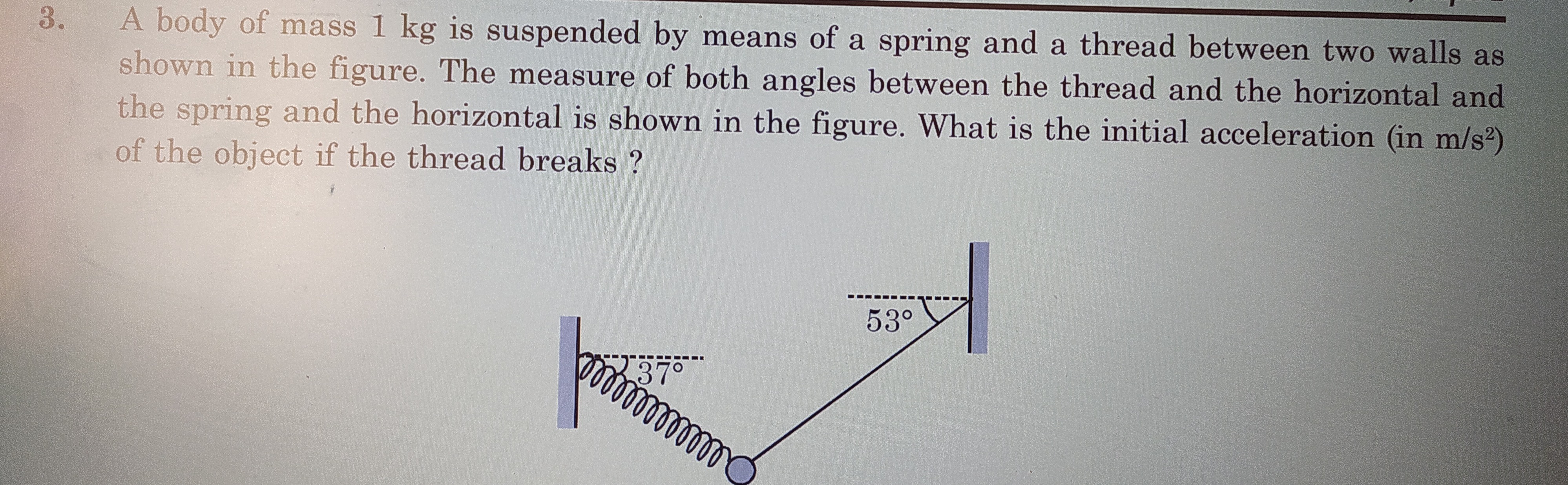
A body of mass 1 kg is suspended by means of a spring and a thread between two walls as shown in the figure. The measure of both angles between the thread and the horizontal and the spring and the horizontal is shown in the figure. What is the initial acceleration (in m/s²) of the object if the thread breaks ?

Answer 1

8

Answer 2

1. Equilibrium Analysis: In equilibrium, the object is acted upon by its weight ($mg$), the tension in the thread ($T$), and the spring force ($F_s$). Resolving forces horizontally and vertically, we get $T \cos(53^\circ) = F_s \cos(37^\circ)$ and $T \sin(53^\circ) + F_s \sin(37^\circ) = mg$. Using trigonometric values for $37^\circ$ and $53^\circ$ (approximated as $\sin 37^\circ = 0.6, \cos 37^\circ = 0.8, \sin 53^\circ = 0.8, \cos 53^\circ = 0.6$), we find $F_s = \frac{3}{5}mg$.

2. Instant of Thread Break: When the thread breaks, the tension $T$ becomes zero. The spring force $F_s$ remains unchanged instantaneously. The forces acting on the object are its weight ($mg$ downwards) and the spring force ($F_s$ at $37^\circ$ to the horizontal).

3. Net Force and Acceleration: The spring force has components $F_s \cos(37^\circ)$ horizontally to the right and $F_s \sin(37^\circ)$ vertically upwards. The weight is $mg$ vertically downwards. The net force components are: $F_{net, x} = F_s \cos(37^\circ)$ $F_{net, y} = F_s \sin(37^\circ) - mg$

4. Calculation: With $m=1$ kg and $g=10$ m/s², $mg = 10$ N. $F_s = \frac{3}{5}mg = \frac{3}{5}(10) = 6$ N. $F_{net, x} = 6 \times (4/5) = 4.8$ N. $F_{net, y} = 6 \times (3/5) - 10 = 3.6 - 10 = -6.4$ N.

5. Initial Acceleration: The acceleration components are $a_x = F_{net, x}/m = 4.8/1 = 4.8$ m/s² and $a_y = F_{net, y}/m = -6.4/1 = -6.4$ m/s². The magnitude of the initial acceleration is $|\vec{a}| = \sqrt{a_x^2 + a_y^2} = \sqrt{(4.8)^2 + (-6.4)^2} = \sqrt{23.04 + 40.96} = \sqrt{64} = 8$ m/s².