Question

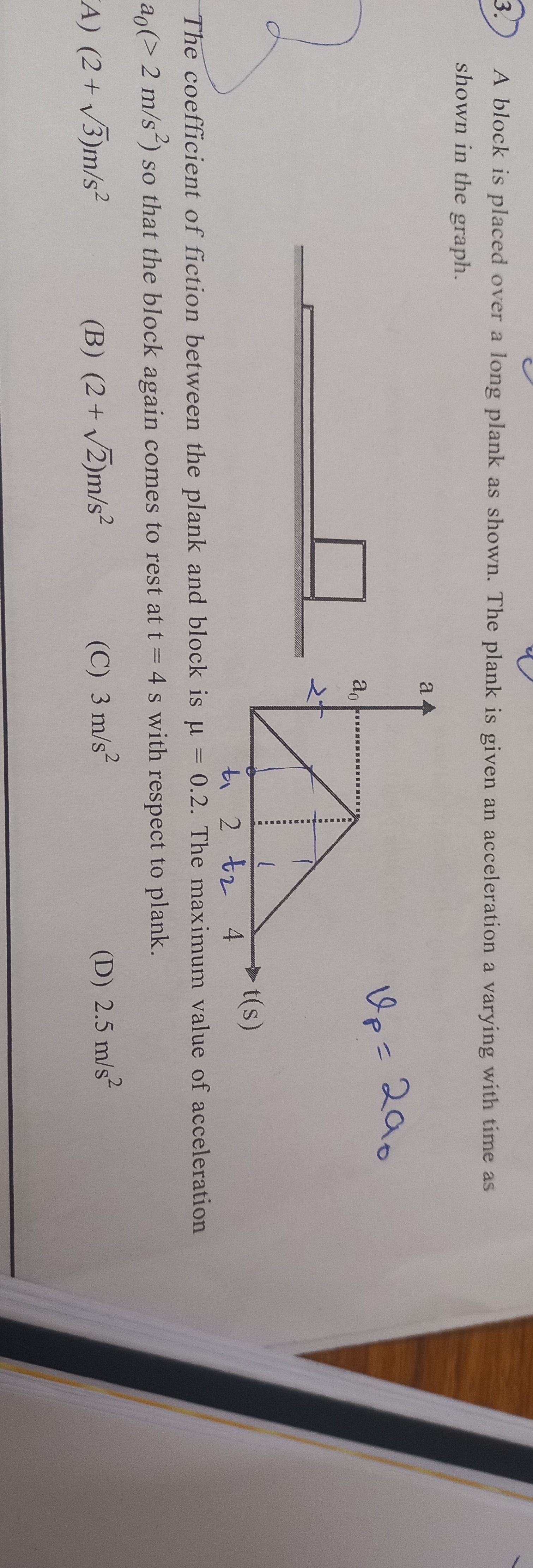
A block is placed over a long plank as shown. The plank is given an acceleration a varying with time as shown in the graph.

The coefficient of friction between the plank and block is μ = 0.2. The maximum value of acceleration ao(> 2 m/s²) so that the block again comes to rest at t = 4 s with respect to plank.

• A. (2 + √3)m/s²
• B. (2 + √2)m/s²
• C. 3 m/s²
• D. 2.5 m/s²

Answer 1

Answer: (B)

(2 + √2)m/s²

Answer 2

The problem asks for the maximum value of acceleration $a_0$ of a plank such that a block placed on it comes to rest relative to the plank at $t=4$ s.

Given: Coefficient of friction $\mu = 0.2$. Acceleration due to gravity $g \approx 10 \, \text{m/s}^2$. Maximum acceleration of the plank $a_0 > 2 \, \text{m/s}^2$.

1. Maximum acceleration due to friction: The maximum acceleration the block can experience due to friction is $a_{fric} = \mu g$. $a_{fric} = 0.2 \times 10 = 2 \, \text{m/s}^2$.

2. Plank's acceleration profile: From the graph, the plank's acceleration $a_p(t)$ varies as: For $0 \le t \le 2$ s: $a_p(t) = \frac{a_0}{2}t$. For $2 \le t \le 4$ s: $a_p(t) = a_0 - \frac{a_0}{2}(t-2) = 2a_0 - \frac{a_0}{2}t$.

3. Slipping condition: Since $a_0 > 2 \, \text{m/s}^2$, the plank's acceleration will exceed $a_{fric} = 2 \, \text{m/s}^2$ at some point. When $a_p(t) > a_{fric}$, the block will slip relative to the plank. Let $t_1$ be the time when slipping begins. At this point, $a_p(t_1) = a_{fric}$. $\frac{a_0}{2}t_1 = 2 \implies t_1 = \frac{4}{a_0}$. Since $a_0 > 2$, $t_1 < 2$ s. So, slipping occurs during the first phase of acceleration.

4. Motion of the block:

   • For $0 \le t \le t_1$: The block moves with the plank, so $v_b(t) = v_p(t)$. $v_p(t) = \int_0^t a_p(\tau) d\tau = \int_0^t \frac{a_0}{2}\tau d\tau = \frac{a_0}{4}t^2$. At $t=t_1$: $v_b(t_1) = v_p(t_1) = \frac{a_0}{4}t_1^2 = \frac{a_0}{4}\left(\frac{4}{a_0}\right)^2 = \frac{4}{a_0}$.
   • For $t_1 < t \le 4$ s: The block slips. The friction force on the block is kinetic friction, which gives the block a constant acceleration $a_b = \mu g = 2 \, \text{m/s}^2$. (The friction acts in the forward direction, trying to accelerate the block with the plank). The velocity of the block at $t=4$ s is: $v_b(4) = v_b(t_1) + \int_{t_1}^4 a_b d\tau = v_b(t_1) + a_b(4 - t_1)$. $v_b(4) = \frac{4}{a_0} + 2\left(4 - \frac{4}{a_0}\right) = \frac{4}{a_0} + 8 - \frac{8}{a_0} = 8 - \frac{4}{a_0}$.

5. Motion of the plank: The velocity of the plank at $t=4$ s is the area under the $a_p-t$ graph from $t=0$ to $t=4$ s. The graph is a triangle with base $4$ s and height $a_0$. $v_p(4) = \frac{1}{2} \times \text{base} \times \text{height} = \frac{1}{2} \times 4 \times a_0 = 2a_0$.

6. Condition for relative rest: For the block to come to rest with respect to the plank at $t=4$ s, their absolute velocities must be equal at $t=4$ s. $v_b(4) = v_p(4)$. $8 - \frac{4}{a_0} = 2a_0$. Multiply by $a_0$ (assuming $a_0 \ne 0$): $8a_0 - 4 = 2a_0^2$. Rearrange into a quadratic equation: $2a_0^2 - 8a_0 + 4 = 0$. Divide by 2: $a_0^2 - 4a_0 + 2 = 0$.

7. Solve the quadratic equation: Using the quadratic formula $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$: $a_0 = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(2)}}{2(1)}$. $a_0 = \frac{4 \pm \sqrt{16 - 8}}{2}$. $a_0 = \frac{4 \pm \sqrt{8}}{2}$. $a_0 = \frac{4 \pm 2\sqrt{2}}{2}$. $a_0 = 2 \pm \sqrt{2}$.

8. Apply the given condition: We are given $a_0 > 2 \, \text{m/s}^2$. The two possible values for $a_0$ are:

   • $a_0 = 2 + \sqrt{2} \approx 2 + 1.414 = 3.414 \, \text{m/s}^2$. This value satisfies $a_0 > 2$.
   • $a_0 = 2 - \sqrt{2} \approx 2 - 1.414 = 0.586 \, \text{m/s}^2$. This value does not satisfy $a_0 > 2$.

Therefore, the maximum value of acceleration $a_0$ is $(2 + \sqrt{2}) \, \text{m/s}^2$.