Question
Question: A block having mass m and charge q is connected by spring of force constant k. The block lies on a f...
A block having mass m and charge q is connected by spring of force constant k. The block lies on a frictionless horizontal track and a uniform electric field E acts on system as shown. The block is released from rest when spring is unstretched (at x=0). Then -
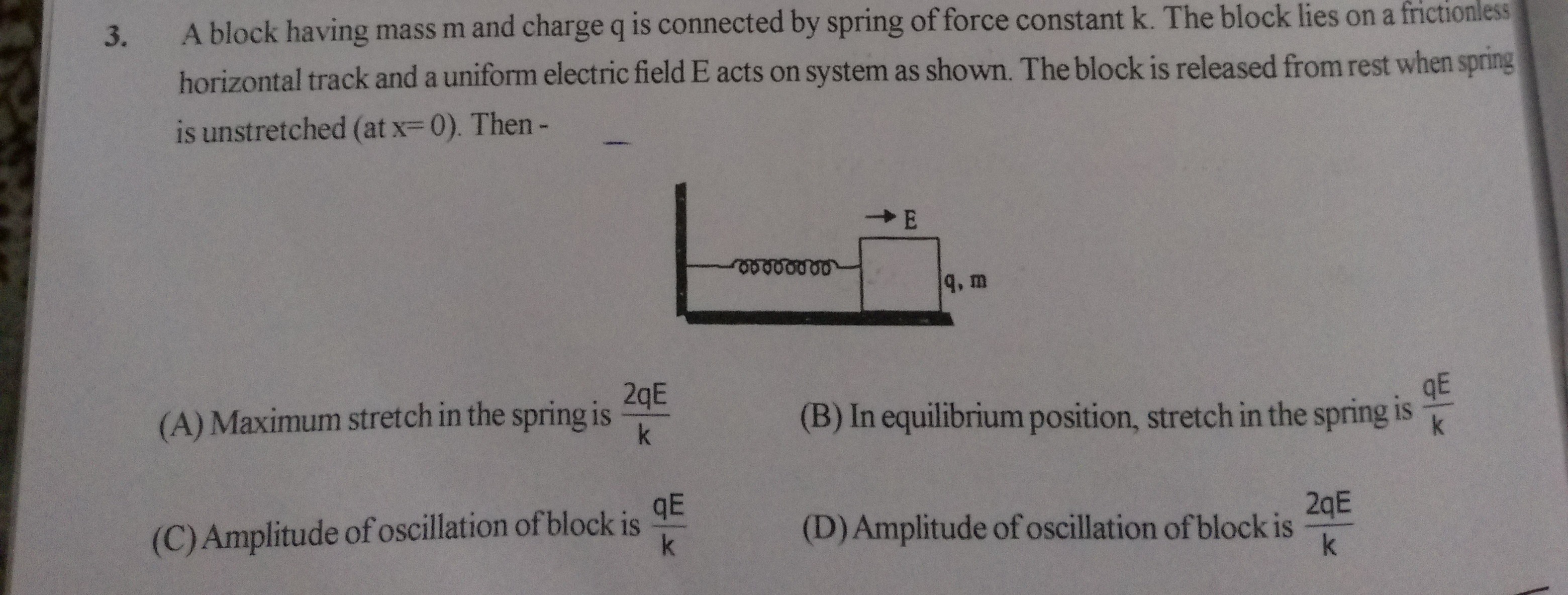
Maximum stretch in the spring is k2qE
In equilibrium position, stretch in the spring is kqE
Amplitude of oscillation of block is kqE
Amplitude of oscillation of block is k2qE
Maximum stretch in the spring is k2qE
In equilibrium position, stretch in the spring is kqE
Amplitude of oscillation of block is kqE
Solution
The block is subjected to two horizontal forces: the electric force Fe=qE and the spring force Fs=−kx.
The equilibrium position xeq is where the net force is zero: qE−kxeq=0 xeq=kqE.
The equation of motion can be rewritten in terms of the displacement from the equilibrium position, x′=x−xeq=x−kqE. The amplitude of oscillation is A=kqE.
Using energy conservation, the maximum stretch in the spring is xmax=k2qE.
