Question

A body of mass 30 kg suspended by means of three strings as shown in figure is in equilibrium. Tension in the horizontal string is (g = 10 m/s²)

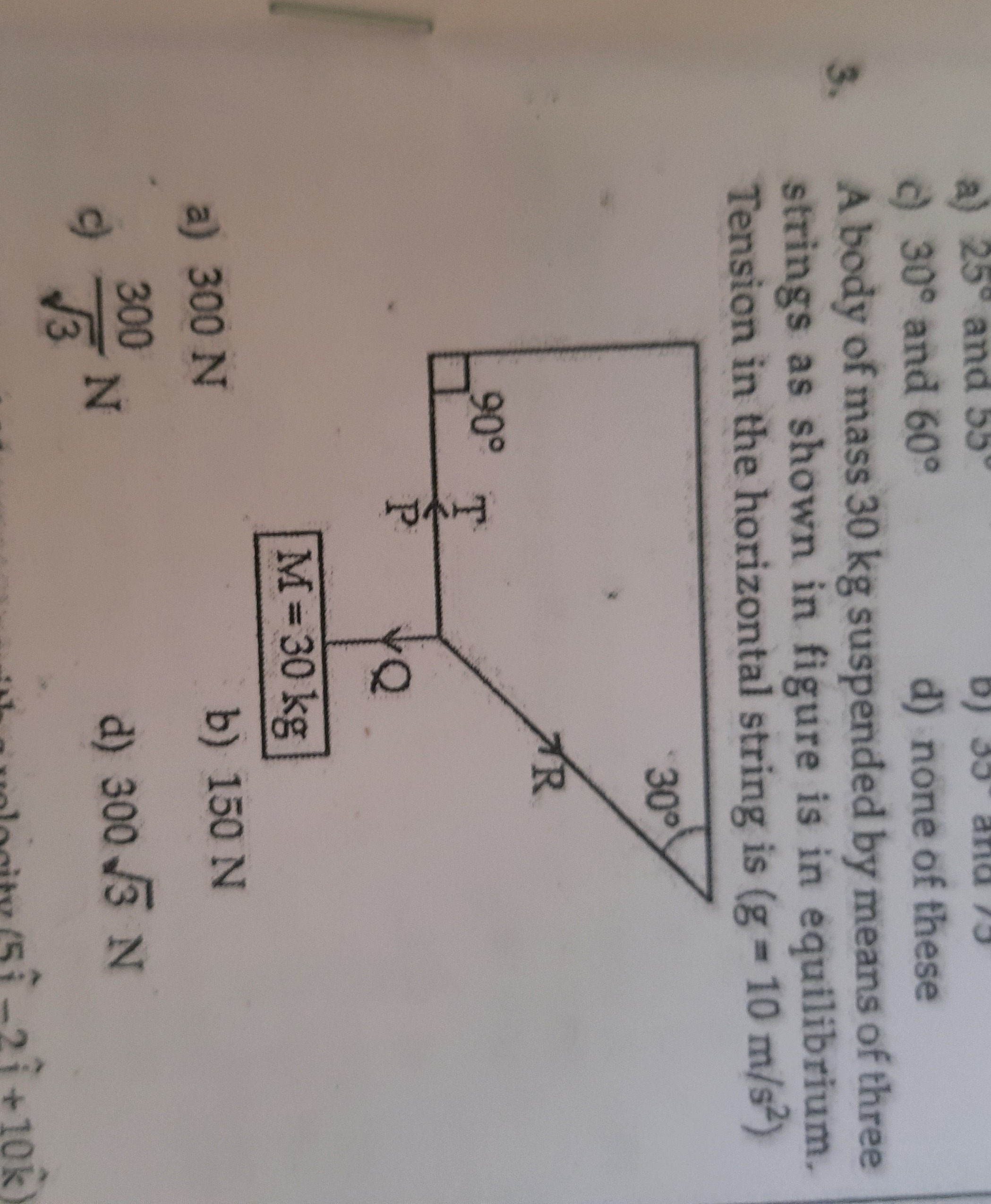
• A. 300 N
• B. 150 N
• C. $\frac{300}{\sqrt{3}}$ N
• D. 300$\sqrt{3}$ N

Answer 1

Answer: (D)

300$\sqrt{3}$ N

Answer 2

We first note that at the point of suspension the three tensions are in equilibrium. In the diagram the vertical string (supporting the 30‐kg mass) provides the upward tension equal to the weight

$W = mg = 30 \times 10 = 300 \, \text{N}$.

At the junction (point Q) the other two strings are:

• A horizontal string with tension $T_h$ (unknown), and
• A string making 30° with the horizontal; call its tension $T_i$.

Since the strings are at right angles (the horizontal and the inclined string make a 90° angle) the vector sum of $T_h$ and $T_i$ must equal the vertical tension needed to balance the weight.

Resolving the inclined tension $T_i$ gives:

Horizontal component = $T_i \cos{30}$ Vertical component = $T_i \sin{30}$

For equilibrium the horizontal components must cancel:

$T_h = T_i \cos{30}$.

Also the entire vertical force is provided solely by the inclined string:

$T_i \sin{30} = 300 \implies T_i = \frac{300}{\sin{30}} = \frac{300}{1/2} = 600 \, \text{N}$.

Thus the tension in the horizontal string is

$T_h = 600 \cos{30} = 600 \times \frac{\sqrt{3}}{2} = 300\sqrt{3} \, \text{N}$.