Question

A particle, which is constrained to move along the x-axis, is subjected to a force in the same direction which varies with the distance $x$ from the origin as $F(x) = -kx + ax^2$. Here $k$ and $a$ are positive constants. For $x \ge 0$, the functional form of the potential energy $U(x)$ of the particle is :

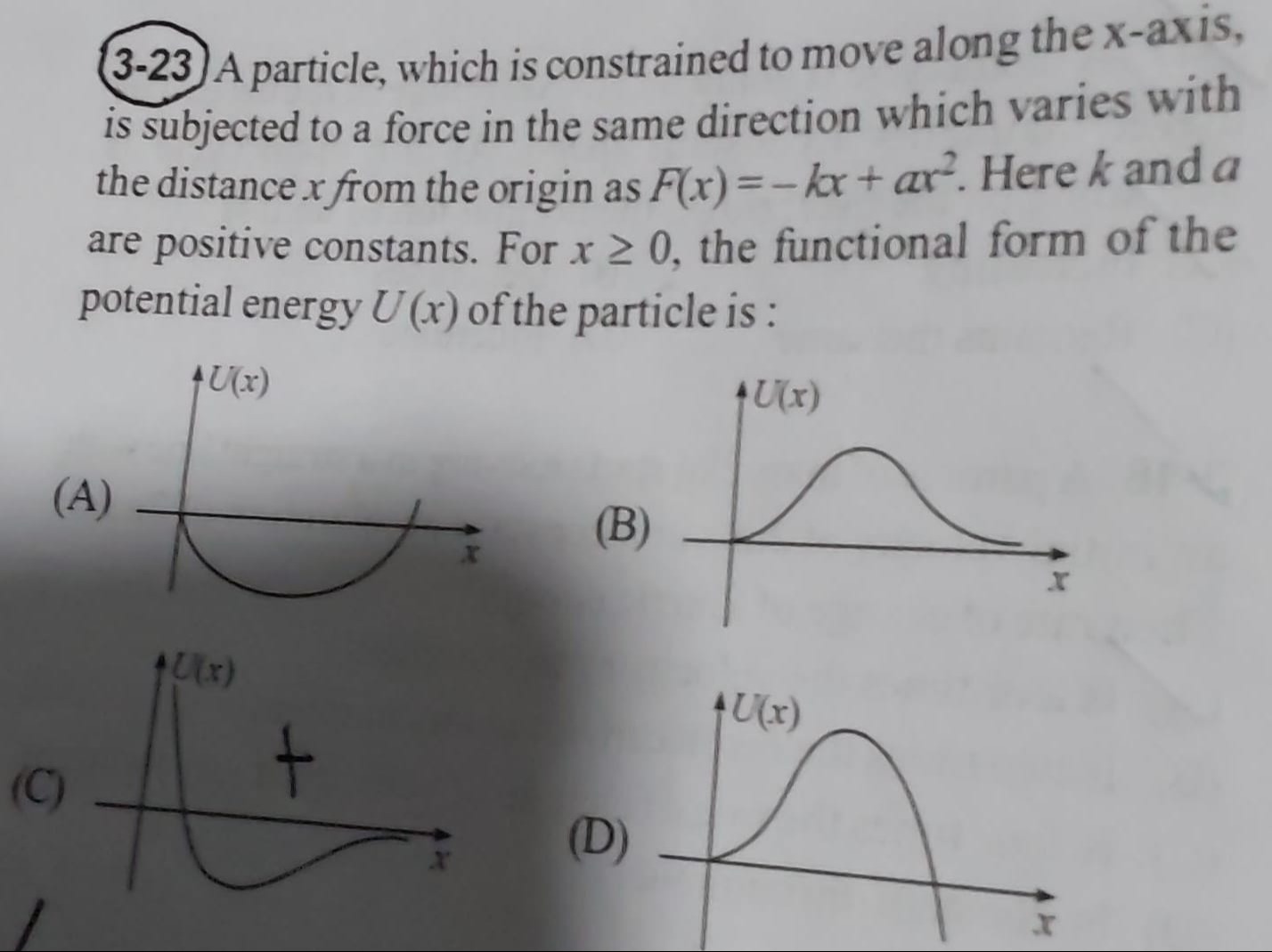
• A. A graph starting at (0,0) with a horizontal tangent, increasing to a maximum, and then decreasing, with a change in concavity from up to down.
• B. A symmetric bell curve that does not go to $-\infty$.
• C. A double potential well.
• D. A graph starting at (0,0) with a horizontal tangent, increasing to a maximum, then decreasing, with concavity that does not match the derived function.

Answer 1

Answer: (A)

A graph starting at (0,0) with a horizontal tangent, increasing to a maximum, and then decreasing, with a change in concavity from up to down.

Answer 2

The relationship between force $F(x)$ and potential energy $U(x)$ is given by $F(x) = -\frac{dU(x)}{dx}$. Given the force $F(x) = -kx + ax^2$, where $k$ and $a$ are positive constants. To find the potential energy, we integrate the negative of the force with respect to $x$: $U(x) = -\int F(x) dx$ $U(x) = -\int (-kx + ax^2) dx$ $U(x) = \int (kx - ax^2) dx$ $U(x) = k \int x dx - a \int x^2 dx$ $U(x) = k \frac{x^2}{2} - a \frac{x^3}{3} + C$

Setting $C=0$ by choosing $U(0)=0$, we get $U(x) = \frac{1}{2}kx^2 - \frac{1}{3}ax^3$.

For $x \ge 0$:

• $U(0) = 0$. The graph starts at the origin with a horizontal tangent.
• Equilibrium points are where $F(x) = 0$: $-kx + ax^2 = 0 \implies x(ax-k) = 0$. So, $x=0$ and $x=k/a$ are equilibrium points.
• The second derivative of potential energy is $\frac{d^2U}{dx^2} = \frac{d}{dx}(kx - ax^2) = k - 2ax$.
• At $x=0$, $\frac{d^2U}{dx^2} = k > 0$, indicating a stable equilibrium (local minimum).
• At $x=k/a$, $\frac{d^2U}{dx^2} = k - 2a(k/a) = k - 2k = -k < 0$, indicating an unstable equilibrium (local maximum).
• Thus, $U(x)$ increases from $x=0$ to $x=k/a$ and decreases for $x > k/a$.
• The concavity changes at $k - 2ax = 0$, which is at $x = k/(2a)$. For $0 \le x < k/(2a)$, the function is concave up. For $x > k/(2a)$, the function is concave down.

Option A correctly depicts a graph starting at the origin with a horizontal tangent, increasing to a maximum at $x=k/a$, decreasing thereafter, and showing a change in concavity from up to down.