Question

$|2|x|+3| < 6$

Answer 1

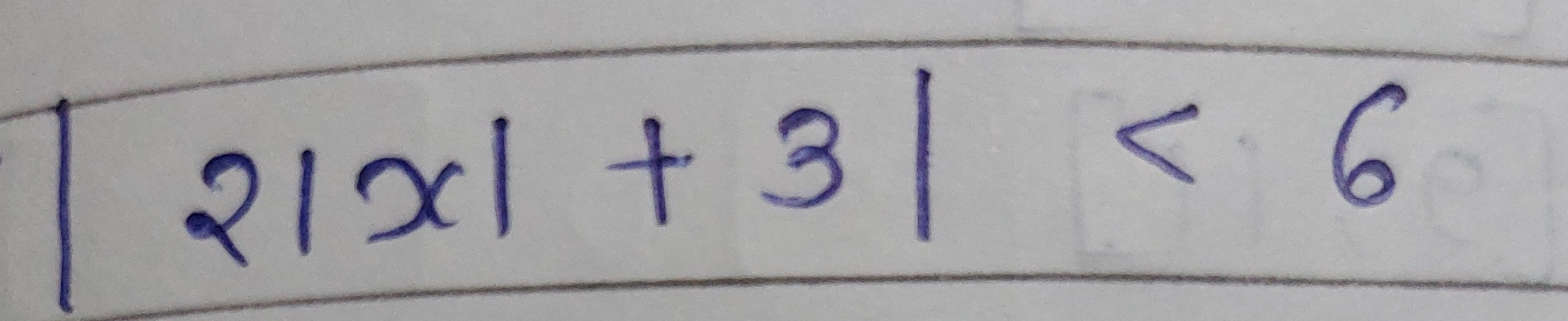
The solution is the interval $(-\frac{3}{2}, \frac{3}{2})$.

Answer 2

The given inequality is $|2|x|+3| < 6$.

We need to solve this inequality for $x$. The expression inside the absolute value is $2|x|+3$. Since $|x| \ge 0$ for any real number $x$, we have $2|x| \ge 0$. Adding 3 to both sides, we get $2|x|+3 \ge 0+3 = 3$. So, the expression $2|x|+3$ is always greater than or equal to 3. This means $2|x|+3$ is always positive.

Since $2|x|+3$ is always positive, its absolute value is equal to the expression itself: $|2|x|+3| = 2|x|+3$.

So, the original inequality $|2|x|+3| < 6$ simplifies to: $2|x|+3 < 6$

Now, we solve this simpler inequality for $|x|$:

Subtract 3 from both sides: $2|x| < 6 - 3$ $2|x| < 3$

Divide by 2: $|x| < \frac{3}{2}$

The inequality $|x| < c$, where $c > 0$, is equivalent to $-c < x < c$. In this case, $c = \frac{3}{2}$. Since $\frac{3}{2} > 0$, we can write: $-\frac{3}{2} < x < \frac{3}{2}$

This is the solution to the inequality. The solution set is the open interval $(-\frac{3}{2}, \frac{3}{2})$.