Question

Solve the following equation:

$2\sqrt{x^2+2x+1}-3\sqrt{x^2-4x+4}+|5-x|=5$

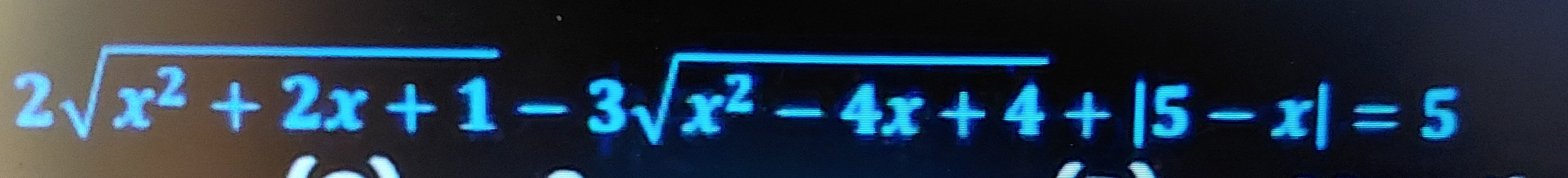
Answer 1

x = 1, 4

Answer 2

The given equation simplifies to $2|x+1|-3|x-2|+|5-x|=5$ by recognizing perfect squares under the square roots. The absolute value equation is solved by considering intervals determined by the roots of the expressions inside the absolute values ($x=-1, 2, 5$). Solving the linear equation in each interval and checking if the solution lies within the interval yields the valid solutions $x=1$ and $x=4$.