Solveeit Logo
Login

Question

Question: $2\log_{4}x - 0.5\log_{2}(x^{2}-3x+2)=0.5$...

2log⁡4x−0.5log⁡2(x2−3x+2)=0.52\log_{4}x - 0.5\log_{2}(x^{2}-3x+2)=0.5

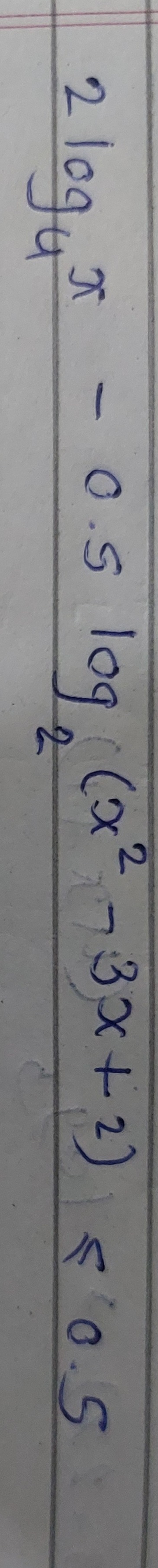
Answer

The solutions are x=3+5x = 3 + \sqrt{5} and x=3−5x = 3 - \sqrt{5}.

Explanation

Solution

  1. Determine the domain of the logarithmic equation by ensuring the arguments of the logarithms are positive.
  2. Convert all logarithms to a common base (base 2 in this case) using the change of base formula.
  3. Simplify the equation using logarithm properties (power rule, quotient rule).
  4. Convert the simplified logarithmic equation into an algebraic equation (a quadratic equation).
  5. Solve the quadratic equation using the quadratic formula.
  6. Check if the solutions obtained are within the domain determined in step 1.