Question
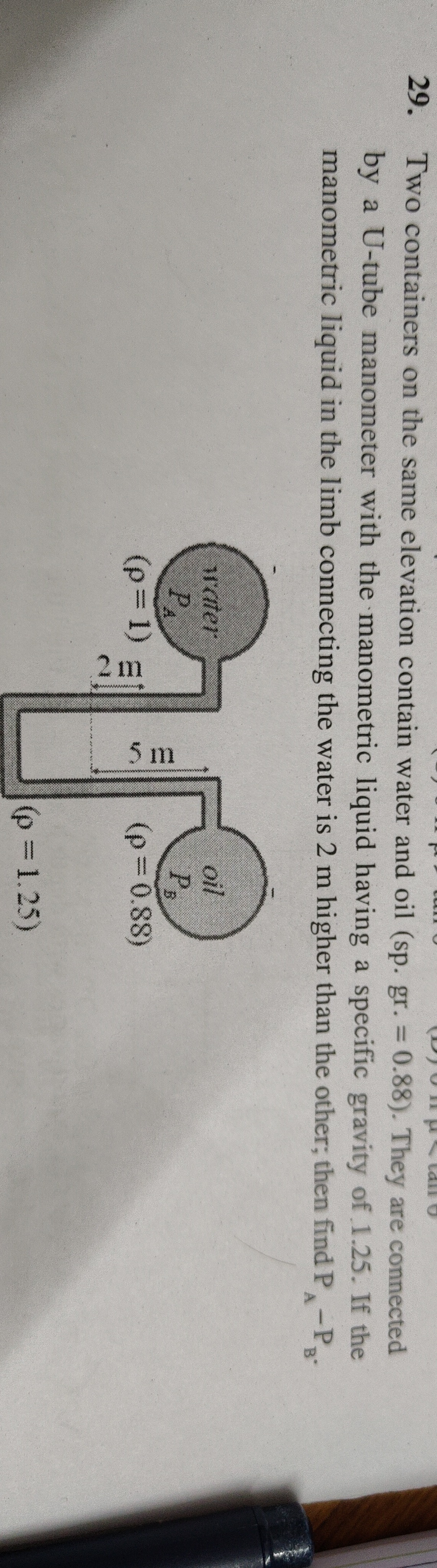
Question: Two containers on the same elevation contain water and oil (sp. gr. = 0.88). They are connected by a...
Two containers on the same elevation contain water and oil (sp. gr. = 0.88). They are connected by a U-tube manometer with the manometric liquid having a specific gravity of 1.25. If the manometric liquid in the limb connecting the water is 2 m higher than the other; then find PA−PB
1.9ρwg or 18620Pa
Solution
We apply the principle of hydrostatic pressure. Let's choose a reference level at the interface between the manometric liquid and the oil.
Pressure from the right side (oil container): Pright=PB+ρoil×g×5
Pressure from the left side (water container), considering the manometric liquid is 2 m higher: Pleft=PA+ρmanometer×g×2
Equating pressures: PB+ρoil×g×5=PA+ρmanometer×g×2
Using specific gravities (Soil=0.88, Smanometer=1.25): ρoil=0.88ρw ρmanometer=1.25ρw
Substituting: PB+(0.88ρw)×g×5=PA+(1.25ρw)×g×2 PB+4.4ρwg=PA+2.5ρwg
Rearranging for PA−PB: PA−PB=4.4ρwg−2.5ρwg PA−PB=1.9ρwg
Using ρw=1000kg/m3 and g=9.8m/s2: PA−PB=1.9×1000×9.8=18620Pa
