Solveeit Logo
Login

Question

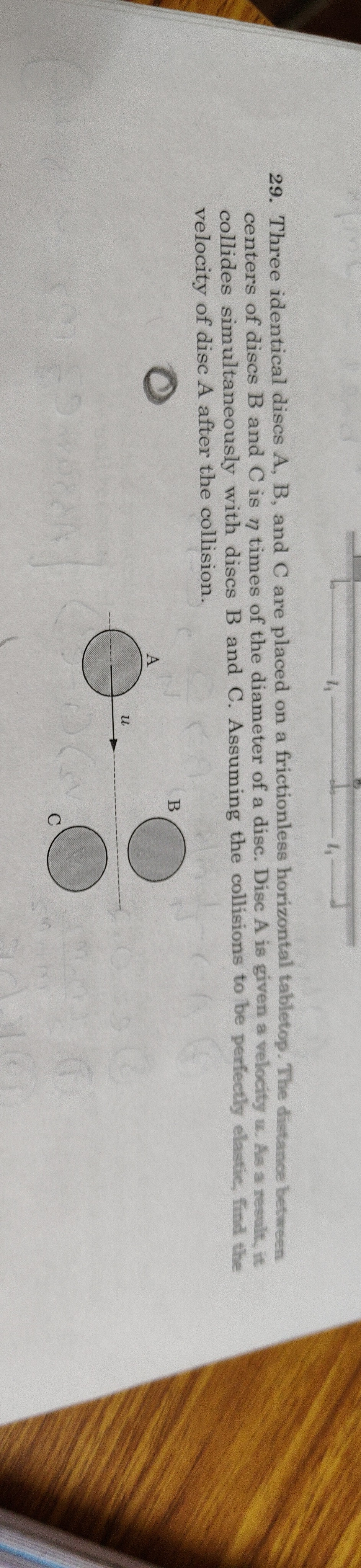
Question: Three identical discs A, B, and C are placed on a frictionless horizontal tabletop. The distance bet...

Three identical discs A, B, and C are placed on a frictionless horizontal tabletop. The distance between centers of discs B and C is nn times of the diameter of a disc. Disc A is given a velocity uu. As a result, it collides simultaneously with discs B and C. Assuming the collisions to be perfectly elastic, find the velocity of disc A after the collision.

Answer

\frac{2-n^2}{6-n^2}u

Explanation

Solution

Let mm be the mass and RR be the radius of each identical disc. The initial velocity of disc A is u⃗A=−uj^\vec{u}_A = -u\hat{j}. Discs B and C are initially at rest. The distance between centers of B and C is 2nR2nR.

  1. Geometry of Collision: For disc A to collide simultaneously with B and C, its center must be at (0,R4−n2)(0, R\sqrt{4-n^2}) at the moment of impact, and the centers of B and C are at (±nR,0)(\pm nR, 0). The angle ϕ\phi between the initial velocity of A (negative y-axis) and the line of impact (from A to B or A to C) is given by sin⁡ϕ=n/2\sin\phi = n/2 and cos⁡ϕ=4−n2/2\cos\phi = \sqrt{4-n^2}/2. This requires n≤2n \le 2.

  2. Conservation of Momentum: Let v⃗A′\vec{v}_A', v⃗B′\vec{v}_B', v⃗C′\vec{v}_C' be the final velocities. mu⃗A=mv⃗A′+mv⃗B′+mv⃗C′m\vec{u}_A = m\vec{v}_A' + m\vec{v}_B' + m\vec{v}_C' Due to symmetry, v⃗A′\vec{v}_A' will be along the y-axis, and v⃗B′=vBx′i^+vBy′j^\vec{v}_B' = v_{Bx}'\hat{i} + v_{By}'\hat{j}, v⃗C′=−vBx′i^+vBy′j^\vec{v}_C' = -v_{Bx}'\hat{i} + v_{By}'\hat{j}. So, −uj^=vA′j^+2vBy′j^-u\hat{j} = v_A'\hat{j} + 2v_{By}'\hat{j}. This gives: vA′+2vBy′=−u(1)v_A' + 2v_{By}' = -u \quad (1)

  3. Conservation of Kinetic Energy (Elastic Collision): 12mu2=12m(vA′)2+12m((vBx′)2+(vBy′)2)+12m((−vBx′)2+(vBy′)2)\frac{1}{2}mu^2 = \frac{1}{2}m(v_A')^2 + \frac{1}{2}m((v_{Bx}')^2 + (v_{By}')^2) + \frac{1}{2}m((-v_{Bx}')^2 + (v_{By}')^2) u2=(vA′)2+2(vBx′)2+2(vBy′)2(2)u^2 = (v_A')^2 + 2(v_{Bx}')^2 + 2(v_{By}')^2 \quad (2)

  4. Relative Velocity along Line of Impact: For perfectly elastic collision, (v⃗B′−v⃗A′)⋅n^AB=u⃗A⋅n^AB(\vec{v}_B' - \vec{v}_A') \cdot \hat{n}_{AB} = \vec{u}_A \cdot \hat{n}_{AB}. Here n^AB=sin⁡ϕi^−cos⁡ϕj^\hat{n}_{AB} = \sin\phi \hat{i} - \cos\phi \hat{j}. u⃗A⋅n^AB=(−uj^)⋅(sin⁡ϕi^−cos⁡ϕj^)=ucos⁡ϕ\vec{u}_A \cdot \hat{n}_{AB} = (-u\hat{j}) \cdot (\sin\phi \hat{i} - \cos\phi \hat{j}) = u\cos\phi. (vBx′i^+(vBy′−vA′)j^)⋅(sin⁡ϕi^−cos⁡ϕj^)=ucos⁡ϕ(v_{Bx}'\hat{i} + (v_{By}' - v_A')\hat{j}) \cdot (\sin\phi \hat{i} - \cos\phi \hat{j}) = u\cos\phi vBx′sin⁡ϕ−(vBy′−vA′)cos⁡ϕ=ucos⁡ϕ(3)v_{Bx}'\sin\phi - (v_{By}' - v_A')\cos\phi = u\cos\phi \quad (3)

Solving (1), (2), (3): From (1), vBy′=−u−vA′2v_{By}' = \frac{-u - v_A'}{2}. Substitute vBy′v_{By}' into (3): vBx′sin⁡ϕ−(−u−vA′2−vA′)cos⁡ϕ=ucos⁡ϕv_{Bx}'\sin\phi - \left(\frac{-u - v_A'}{2} - v_A'\right)\cos\phi = u\cos\phi vBx′sin⁡ϕ+u+3vA′2cos⁡ϕ=ucos⁡ϕv_{Bx}'\sin\phi + \frac{u + 3v_A'}{2}\cos\phi = u\cos\phi vBx′=u−3vA′2cot⁡ϕv_{Bx}' = \frac{u - 3v_A'}{2}\cot\phi.

Substitute vBy′v_{By}' and vBx′v_{Bx}' into (2): u2=(vA′)2+2(u−3vA′2cot⁡ϕ)2+2(−u−vA′2)2u^2 = (v_A')^2 + 2\left(\frac{u - 3v_A'}{2}\cot\phi\right)^2 + 2\left(\frac{-u - v_A'}{2}\right)^2 u2=(vA′)2+(u−3vA′)22cot⁡2ϕ+(u+vA′)22u^2 = (v_A')^2 + \frac{(u - 3v_A')^2}{2}\cot^2\phi + \frac{(u + v_A')^2}{2} Using cot⁡2ϕ=cos⁡2ϕsin⁡2ϕ=(4−n2)/4n2/4=4−n2n2\cot^2\phi = \frac{\cos^2\phi}{\sin^2\phi} = \frac{(4-n^2)/4}{n^2/4} = \frac{4-n^2}{n^2}: 2u2=2(vA′)2+(u−3vA′)2(4−n2n2)+(u+vA′)22u^2 = 2(v_A')^2 + (u - 3v_A')^2\left(\frac{4-n^2}{n^2}\right) + (u + v_A')^2 Multiply by n2n^2: 2u2n2=2(vA′)2n2+(u−3vA′)2(4−n2)+(u+vA′)2n22u^2n^2 = 2(v_A')^2n^2 + (u - 3v_A')^2(4-n^2) + (u + v_A')^2n^2 Expanding and rearranging into a quadratic equation for vA′v_A': (18−3n2)(vA′)2+(4n2−12)uvA′+(2−n2)u2=0(18 - 3n^2)(v_A')^2 + (4n^2 - 12)uv_A' + (2 - n^2)u^2 = 0 Let x=vA′/ux = v_A'/u. (18−3n2)x2+(4n2−12)x+(2−n2)=0(18 - 3n^2)x^2 + (4n^2 - 12)x + (2 - n^2) = 0 Solving this quadratic equation for xx: x=−(4n2−12)±(4n2−12)2−4(18−3n2)(2−n2)2(18−3n2)x = \frac{-(4n^2 - 12) \pm \sqrt{(4n^2 - 12)^2 - 4(18 - 3n^2)(2 - n^2)}}{2(18 - 3n^2)} x=12−4n2±16(n2−3)2−12(6−n2)(2−n2)6(6−n2)x = \frac{12 - 4n^2 \pm \sqrt{16(n^2 - 3)^2 - 12(6 - n^2)(2 - n^2)}}{6(6 - n^2)} x=12−4n2±16(n4−6n2+9)−12(12−8n2+n4)6(6−n2)x = \frac{12 - 4n^2 \pm \sqrt{16(n^4 - 6n^2 + 9) - 12(12 - 8n^2 + n^4)}}{6(6 - n^2)} x=12−4n2±16n4−96n2+144−144+96n2−12n46(6−n2)x = \frac{12 - 4n^2 \pm \sqrt{16n^4 - 96n^2 + 144 - 144 + 96n^2 - 12n^4}}{6(6 - n^2)} x=12−4n2±4n46(6−n2)x = \frac{12 - 4n^2 \pm \sqrt{4n^4}}{6(6 - n^2)} x=12−4n2±2n26(6−n2)x = \frac{12 - 4n^2 \pm 2n^2}{6(6 - n^2)}

Two solutions for xx: x1=12−4n2+2n26(6−n2)=12−2n26(6−n2)=2(6−n2)6(6−n2)=13x_1 = \frac{12 - 4n^2 + 2n^2}{6(6 - n^2)} = \frac{12 - 2n^2}{6(6 - n^2)} = \frac{2(6 - n^2)}{6(6 - n^2)} = \frac{1}{3} x2=12−4n2−2n26(6−n2)=12−6n26(6−n2)=6(2−n2)6(6−n2)=2−n26−n2x_2 = \frac{12 - 4n^2 - 2n^2}{6(6 - n^2)} = \frac{12 - 6n^2}{6(6 - n^2)} = \frac{6(2 - n^2)}{6(6 - n^2)} = \frac{2 - n^2}{6 - n^2}

The solution x1=1/3x_1 = 1/3 implies vA′=u/3v_A' = u/3. This would mean vBx′=0v_{Bx}'=0 (as u−3vA′2cot⁡ϕ=0\frac{u-3v_A'}{2}\cot\phi = 0). For an oblique collision (where n>0n>0), the discs B and C must acquire a component of velocity perpendicular to the initial line of motion of A. Thus, vBx′v_{Bx}' cannot be zero unless n=2n=2 (where cot⁡ϕ=0\cot\phi=0). If n=2n=2, this solution is valid. The solution x2=2−n26−n2x_2 = \frac{2-n^2}{6-n^2} is the general solution for the velocity of A. For n=2n=2, x2=2−46−4=−22=−1x_2 = \frac{2-4}{6-4} = \frac{-2}{2} = -1. This means vA′=−uv_A' = -u, which implies disc A reverses its velocity and B and C remain at rest (as shown by substituting vA′=−uv_A'=-u into (1) and (3), which gives vB′=vC′=0v_B'=v_C'=0). This is the trivial solution or the initial state, which is not what happens after a collision where energy is transferred. Therefore, the physically meaningful solution for vA′v_A' is u2−n26−n2u \frac{2-n^2}{6-n^2}. The velocity of disc A after collision is v⃗A′=u⃗(2−n26−n2)\vec{v}_A' = \vec{u} \left(\frac{2-n^2}{6-n^2}\right).

The final answer is 2−n26−n2u\boxed{\frac{2-n^2}{6-n^2}u}