Question

Range of the function $f(x) = \log_2 \left(\frac{4}{\sqrt{x+2} + \sqrt{2-x}}\right)$ is:

Answer 1

$\left[\frac{1}{2}, 1\right]$

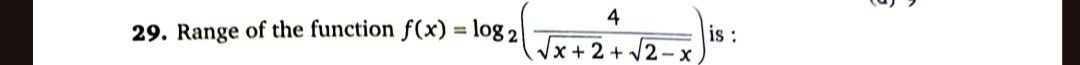
Answer 2

1. Find the domain of the function $f(x)$. The domain is $[-2, 2]$.

2. Let $g(x) = \sqrt{x+2} + \sqrt{2-x}$. Find the range of $g(x)$ on the domain $[-2, 2]$. By squaring $g(x)$, we found that $g(x)^2 \in [4, 8]$, so $g(x) \in [2, 2\sqrt{2}]$.

3. The argument of the logarithm is $\frac{4}{g(x)}$. Determine the range of this argument. Since $g(x) \in [2, 2\sqrt{2}]$, the argument $\frac{4}{g(x)} \in \left[\frac{4}{2\sqrt{2}}, \frac{4}{2}\right] = [\sqrt{2}, 2]$.

4. The function is $f(x) = \log_2(y)$, where $y$ is the argument of the logarithm. Since $y \in [\sqrt{2}, 2]$ and $\log_2(y)$ is an increasing function, the range of $f(x)$ is $[\log_2(\sqrt{2}), \log_2(2)] = \left[\frac{1}{2}, 1\right]$.