Question

$\frac{1}{x+\sqrt{x}}$

Answer 1

$\frac{x-\sqrt{x}}{x(x-1)}$

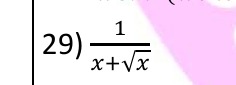
Answer 2

To simplify the expression $\frac{1}{x+\sqrt{x}}$, we follow these steps:

1. Factor the denominator:
   The denominator is $x+\sqrt{x}$. We can rewrite $x$ as $(\sqrt{x})^2$.
   So, $x+\sqrt{x} = (\sqrt{x})^2 + \sqrt{x}$.
   Factor out $\sqrt{x}$ from both terms:
   $x+\sqrt{x} = \sqrt{x}(\sqrt{x} + 1)$.

2. Substitute the factored denominator back into the expression:
   $\frac{1}{x+\sqrt{x}} = \frac{1}{\sqrt{x}(\sqrt{x} + 1)}$.

This form is considered a simplified form as the denominator is factored. If the goal is to rationalize the denominator (remove all radicals from the denominator), further steps would be required:

3. Rationalize the denominator:
   To remove $\sqrt{x}$ from the denominator, multiply by $\sqrt{x}$.
   To remove $\sqrt{x}+1$ from the denominator, multiply by its conjugate, $\sqrt{x}-1$.
   So, multiply the numerator and denominator by $\sqrt{x}(\sqrt{x}-1)$:
   $\frac{1}{\sqrt{x}(\sqrt{x} + 1)} \times \frac{\sqrt{x}(\sqrt{x}-1)}{\sqrt{x}(\sqrt{x}-1)}$
   $= \frac{\sqrt{x}(\sqrt{x}-1)}{(\sqrt{x})^2 (\sqrt{x}+1)(\sqrt{x}-1)}$
   $= \frac{x-\sqrt{x}}{x(x-1)}$

Both $\frac{1}{\sqrt{x}(\sqrt{x} + 1)}$ and $\frac{x-\sqrt{x}}{x(x-1)}$ are simplified forms. The latter has a rational denominator. In the context of JEE/NEET, "simplify" often implies rationalizing the denominator if it contains radicals.