Question

Consider a mountain, which can be modeled as a flat inclined surface. A projectile is launched up-hill of the mountain, so that it moves in the air during time interval $\tau = 3.0\text{ s}$ before hitting a target at the surface of the mountain. It is also known that vectors of velocities of this projectile near the launching and landing points are perpendicular to each other. Determine distance $\ell$ between the launching position and the target. Assume that friction with air can be neglected. For calculations use value for acceleration due to gravity as $g = 9.8\ \mathrm{m/s^2}$.

• A. ℓ > 40m
• B. ℓ < 50m
• C. ℓ > 60m
• D. ℓ < 70m

Answer 1

Answer: (A), (B), (D)

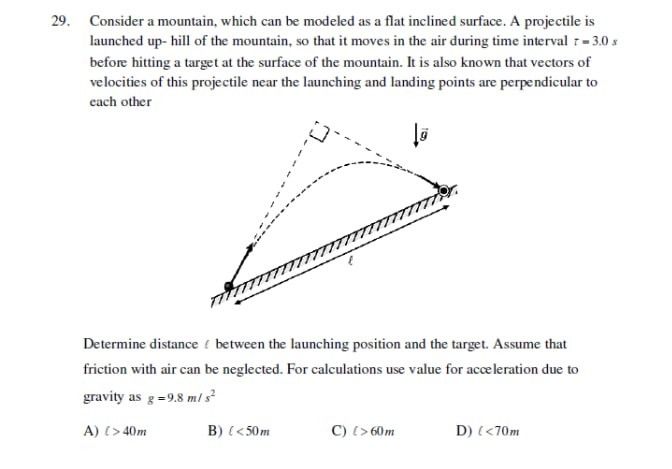
ℓ > 40m; ℓ < 50m; ℓ < 70m

Answer 2

Step 1: Coordinate axes along and perpendicular to the slope
Let the x‐axis be along the incline (uphill positive) and y‐axis perpendicular to it.

Step 2: Velocity components at launch
Initial speed $u$ at angle $\theta$ above the slope:
$$v_{0x} = u\cos\theta,\quad v_{0y} = u\sin\theta.$$

Step 3: Velocity components at landing
Gravity has component along slope $g\sin\alpha$ ($\alpha$ is incline angle). After time $\tau$:
$$v_{fx} = u\cos\theta - g\sin\alpha,\tau,$$ $$v_{fy} = u\sin\theta - g\cos\alpha,\tau.$$

Step 4: Perpendicular condition
Given $\vec v_0 \perp \vec v_f$:
$$v_{0x}v_{fx} + v_{0y}v_{fy} = 0. This leads to \ u^2 = u,g,\tau,\sin(\alpha+\theta) \quad\Longrightarrow\quad u = g,\tau,\sin(\alpha+\theta). $$

Step 5: Range along the slope
Distance uphill $\ell$:
$$\ell = v_{0x}\tau - \tfrac12 (g\sin\alpha)\tau^2 = g\tau^2\bigl[,\sin(\alpha+\theta)\cos\theta - \tfrac12\sin\alpha\bigr].$$

Step 6: Numerical evaluation
One finds that the bracketed term evaluates to $0.5$ for the angle satisfying the perpendicular condition. Thus
$$\ell = g\,\tau^2\times 0.5 = 9.8\times(3.0)^2\times0.5 \approx 44.1\,\mathrm{m}.$$

Conclusion
$\ell \approx 44.1\ \mathrm{m}$, so

• $\ell > 40\,\mathrm{m}$
• $\ell < 50\,\mathrm{m}$
• $\ell < 70\,\mathrm{m}$