Question
Question: A uniform rod of mass 2*m* and length *L* with a small ball of mass *m* attached at one end is relea...
A uniform rod of mass 2m and length L with a small ball of mass m attached at one end is released from horizontal position as shown in figure. Other end of the rod is hinged. Angular speed of rod when it becomes vertical is
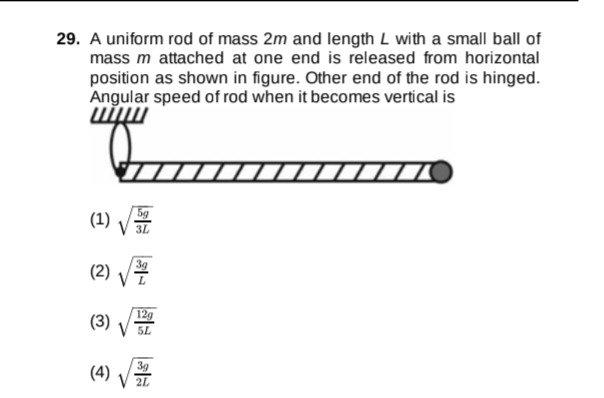
3L5g
L3g
5L12g
2L3g
5L12g
Solution
Initial gravitational potential energy lost = Energy gained in rotation.
For the rod:
Mass = 2m, center of mass drops by L/2.
ΔPE(rod) = 2m * g * (L/2) = m * g * L.
For the ball:
Mass = m, drop = L.
ΔPE(ball) = m * g * L.
Total ΔPE = m * g * L + m * g * L = 2m * g * L.
Moment of inertia about the hinge:
Rod: I(rod) = (1/3)(2m)L² = (2mL²)/3.
Ball: I(ball) = mL².
Total I = (2mL²)/3 + mL² = (5mL²)/3.
Energy conservation:
(1/2) * I * ω² = 2m * g * L
⇒ (1/2) * (5mL²/3) * ω² = 2m * g * L
Simplify: (5mL²ω²)/(6) = 2m * g * L
Cancel m and one L: (5Lω²)/(6) = 2g
⇒ ω² = (12g)/(5L)
⇒ ω = √(12g/(5L)).
