Question

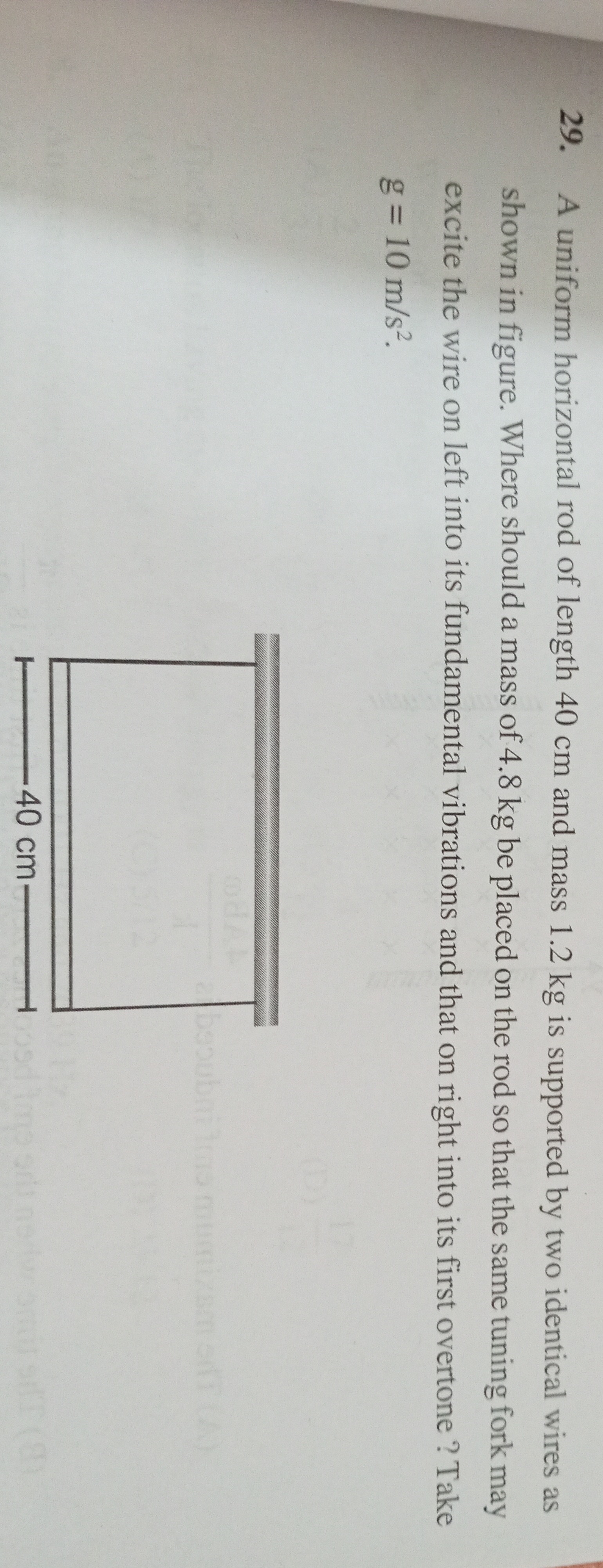
A uniform horizontal rod of length 40 cm and mass 1.2 kg is supported by two identical wires as shown in figure. Where should a mass of 4.8 kg be placed on the rod so that the same tuning fork may excite the wire on left into its fundamental vibrations and that on right into its first overtone ? Take g = 10 m/s².

Answer 1

5 cm from the left end

Answer 2

The frequency of vibration of a stretched wire is given by $f = \frac{n}{2l} \sqrt{\frac{T}{\mu}}$, where $n$ is the mode number, $l$ is the length of the wire, $T$ is the tension in the wire, and $\mu$ is the linear mass density of the wire.

The two wires are identical, so they have the same length $l$ and linear mass density $\mu$.

The left wire is in its fundamental vibration, so $n_1 = 1$. Its frequency is $f_1 = \frac{1}{2l} \sqrt{\frac{T_1}{\mu}}$.

The right wire is in its first overtone, so $n_2 = 2$. Its frequency is $f_2 = \frac{2}{2l} \sqrt{\frac{T_2}{\mu}} = \frac{1}{l} \sqrt{\frac{T_2}{\mu}}$.

Since the same tuning fork excites both wires, $f_1 = f_2$.

$\frac{1}{2l} \sqrt{\frac{T_1}{\mu}} = \frac{1}{l} \sqrt{\frac{T_2}{\mu}}$

$\frac{1}{2} \sqrt{T_1} = \sqrt{T_2}$

$\sqrt{T_1} = 2 \sqrt{T_2}$

$T_1 = 4T_2$.

Let the length of the rod be $L = 40$ cm $= 0.4$ m. The mass of the rod is $M = 1.2$ kg. The rod is uniform, so its weight $Mg$ acts at the center, which is at $L/2 = 20$ cm from either end. The mass to be placed is $m = 4.8$ kg. Let the mass $m$ be placed at a distance $x$ from the left end of the rod.

For vertical equilibrium of the rod, the sum of upward forces equals the sum of downward forces:

$T_1 + T_2 = Mg + mg$

Substitute $T_1 = 4T_2$:

$4T_2 + T_2 = (M+m)g$

$5T_2 = (M+m)g$

$T_2 = \frac{(M+m)g}{5}$

$T_1 = 4T_2 = \frac{4(M+m)g}{5}$.

For rotational equilibrium, the sum of torques about any point is zero. Let's take the torques about the left end of the rod.

The tension $T_1$ acts at the left end, so its torque is zero.

The weight of the rod $Mg$ acts at the center, distance $L/2$ from the left end. The torque is $(Mg) \times (L/2)$.

The weight of the mass $mg$ acts at distance $x$ from the left end. The torque is $(mg) \times x$.

The tension $T_2$ acts at the right end, distance $L$ from the left end. The torque is $(T_2) \times L$.

Taking the left end as the pivot, the clockwise torques are due to the weights, and the counter-clockwise torque is due to $T_2$.

$(Mg) \times (L/2) + (mg) \times x = T_2 \times L$

Substitute the values: $M = 1.2$ kg, $m = 4.8$ kg, $L = 0.4$ m, $g = 10$ m/s².

$T_2 = \frac{(1.2+4.8) \times 10}{5} = \frac{6.0 \times 10}{5} = \frac{60}{5} = 12$ N.

$(1.2 \times 10) \times (0.4/2) + (4.8 \times 10) \times x = 12 \times 0.4$

$12 \times 0.2 + 48 \times x = 4.8$

$2.4 + 48x = 4.8$

$48x = 4.8 - 2.4$

$48x = 2.4$

$x = \frac{2.4}{48} = \frac{24}{480} = \frac{1}{20} = 0.05$ m.

The distance $x$ is measured from the left end. So the mass should be placed at a distance of 0.05 m = 5 cm from the left end of the rod.