Question
Question: $^{28}C_4 = ^9C_b$ Find max value of $a+b$. ...
28C4=9Cb Find max value of a+b.
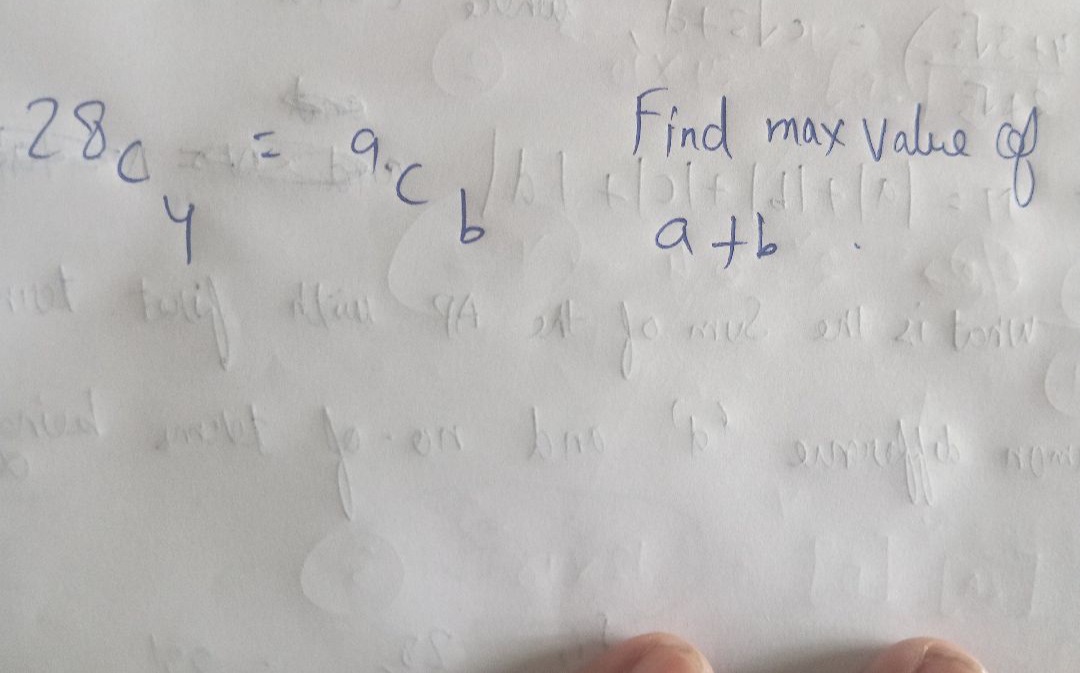
32
52
13
14
52
Solution
The given equation is 28C4=9Cb. We are asked to find the maximum value of a+b.
First, let's calculate the value of 28C4: 28C4=4!(28−4)!28!=4×3×2×128×27×26×25=7×9×13×25=20475
Now, the equation becomes: 20475=9Cb
The maximum value 9Cb can take is 9C4 or 9C5, which is 126. Since 20475>126, there is no integer solution for b in the given equation.
This indicates a likely typo in the question. A common pattern in such problems is that the bases of the combinations are the same. Let's assume the question was intended to be: 28C4=28Cb In this context, we can infer that a=28.
From the property of combinations, if nCr=nCs, then either r=s or r+s=n. Applying this to 28C4=28Cb:
- b=4
- b=28−4=24
We need to find the maximum value of a+b. Case 1: a=28 and b=4. Then a+b=28+4=32. Case 2: a=28 and b=24. Then a+b=28+24=52.
The maximum value of a+b is 52.
