Question

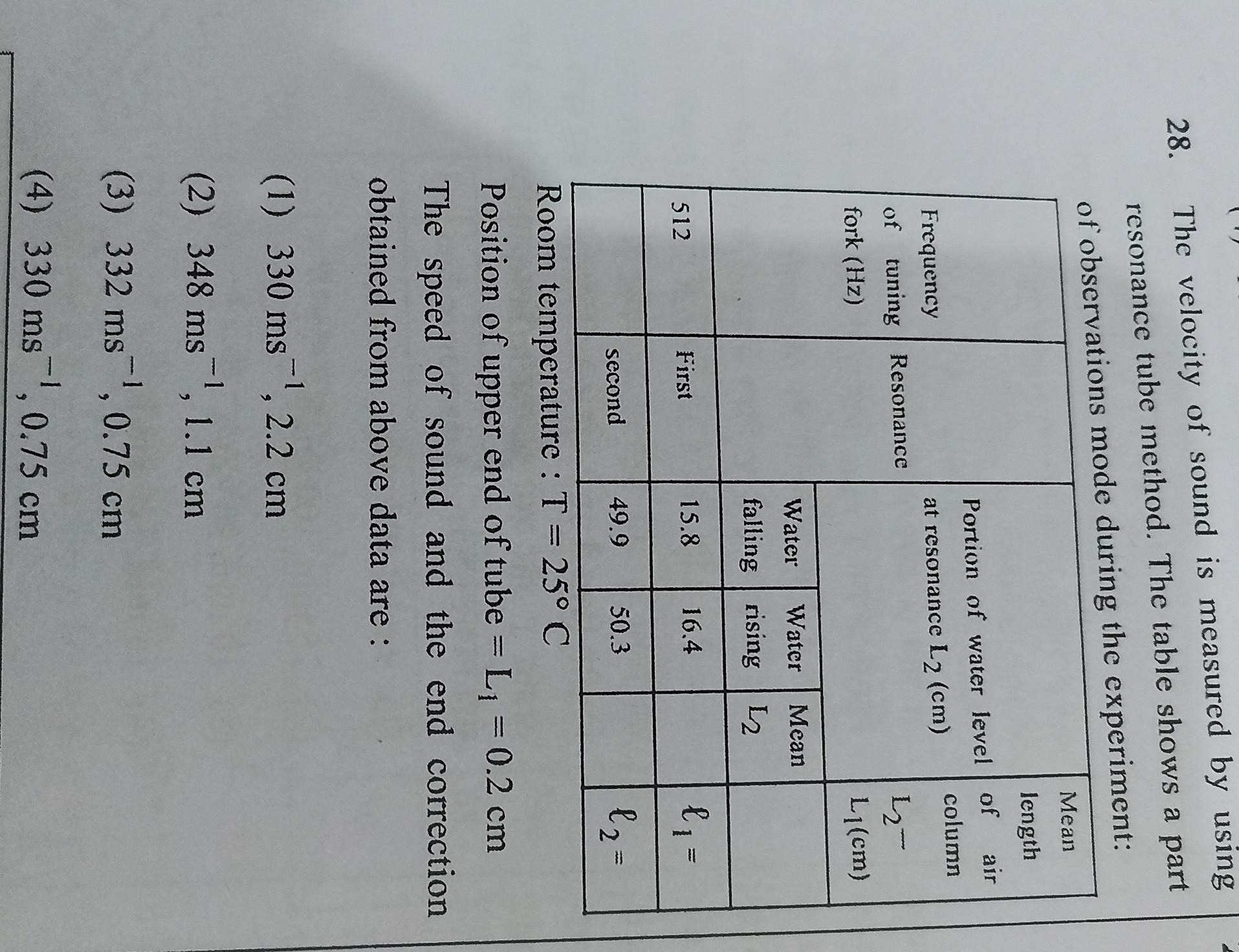
The velocity of sound is measured by using resonance tube method. The table shows a part of observations mode during the experiment:

[Image of a table with columns for "Length of air column (cm)" and "Frequency (Hz)". The table has rows for "First resonance", "Second resonance", and "Third resonance". The values for "First resonance" are 15.8 and 16.4. The values for "Second resonance" are 49.9 and 50.3. The values for "Third resonance" are 84.3 and 84.7. The frequency for all resonances is 512 Hz.]

Room temperature : T = 25° С

Position of upper end of tube = L₁ = 0.2 cm

The speed of sound and the end correction obtained from above data are :

• A. 330 ms⁻¹, 2.2 cm
• B. 348 ms⁻¹, 1.1 cm
• C. 332 ms⁻¹, 0.75 cm
• D. 330 ms⁻¹, 0.75 cm

Answer 1

Answer: (B)

348 ms⁻¹, 1.1 cm

Answer 2

The resonance tube acts as a closed organ pipe. The conditions for resonance are $l + e = (2n-1)\frac{\lambda}{4}$, where $l$ is the length of the air column, $e$ is the end correction, $\lambda$ is the wavelength, and $n$ is the order of resonance.

The mean lengths of the air column for the first and second resonances are calculated as: $l_1 = \frac{15.8 + 16.4}{2} = 16.1$ cm $l_2 = \frac{49.9 + 50.3}{2} = 50.1$ cm

For the first resonance ($n=1$): $l_1 + e = \frac{\lambda}{4}$ For the second resonance ($n=2$): $l_2 + e = \frac{3\lambda}{4}$

Subtracting the first equation from the second gives: $l_2 - l_1 = \frac{3\lambda}{4} - \frac{\lambda}{4} = \frac{2\lambda}{4} = \frac{\lambda}{2}$

Substituting the measured values: $50.1 \text{ cm} - 16.1 \text{ cm} = 34.0 \text{ cm} = \frac{\lambda}{2}$ Thus, the wavelength is $\lambda = 2 \times 34.0 \text{ cm} = 68.0$ cm.

The speed of sound is $v = f\lambda$. Given $f = 512$ Hz and $\lambda = 68.0$ cm: $v = 512 \text{ Hz} \times 68.0 \text{ cm} = 34816 \text{ cm/s} = 348.16 \text{ m/s}$

Using the first resonance condition to find the end correction: $l_1 + e = \frac{\lambda}{4}$ $16.1 \text{ cm} + e = \frac{68.0 \text{ cm}}{4} = 17.0 \text{ cm}$ So, $e = 17.0 \text{ cm} - 16.1 \text{ cm} = 0.9 \text{ cm}$.

The calculated values are approximately $v = 348 \text{ m/s}$ and $e = 0.9 \text{ cm}$. Option (2) provides $v = 348 \text{ m/s}$ and $e = 1.1 \text{ cm}$. The speed of sound matches very closely. Considering experimental errors, option (2) is the most plausible answer.