Question

The number $N = \frac{1+2\log_3 2}{(1 + \log_3 2)^2} + \log_6^2 2$ when simplified reduces to -

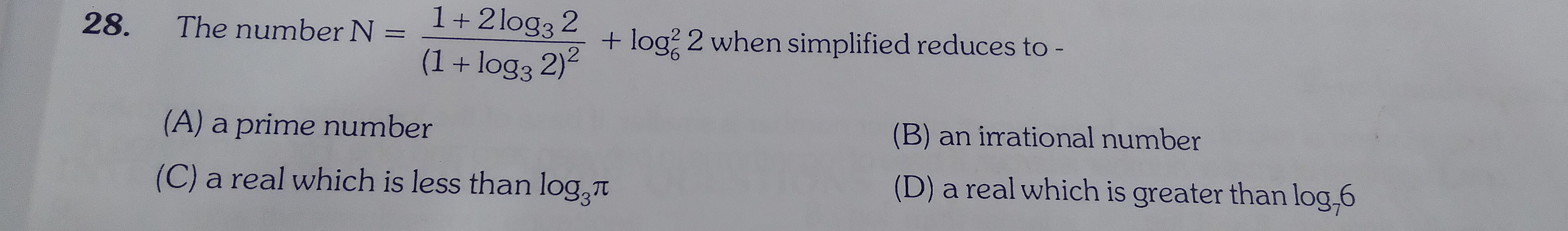
• A. a prime number
• B. an irrational number
• C. a real which is less than $\log_3 \pi$
• D. a real which is greater than $\log_7 6$

Answer 1

Answer: (C), (D)

C and D

Answer 2

Let $x = \log_3 2$. The first term is $\frac{1+2x}{(1+x)^2} = 1 - \left(\frac{x}{1+x}\right)^2$. Since $1+x = 1 + \log_3 2 = \log_3 3 + \log_3 2 = \log_3 6$, we have $\frac{x}{1+x} = \frac{\log_3 2}{\log_3 6} = \log_6 2$. So the first term is $1 - (\log_6 2)^2$. The second term is $(\log_6 2)^2$. Thus, $N = (1 - (\log_6 2)^2) + (\log_6 2)^2 = 1$.

Check options: (A) 1 is not prime. (B) 1 is rational. (C) $1 < \log_3 \pi \iff 3^1 < \pi \iff 3 < \pi$, which is true. (D) $1 > \log_7 6 \iff 7^1 > 6 \iff 7 > 6$, which is true.