Solveeit Logo
Login

Question

Question: $\lim_{x\to 1^-} \left( \frac{2}{\pi}sin^{-1}x \right)^{\sqrt{-cot\pi x}}$...

lim⁡x→1−(2πsin−1x)−cotπx\lim_{x\to 1^-} \left( \frac{2}{\pi}sin^{-1}x \right)^{\sqrt{-cot\pi x}}

Answer

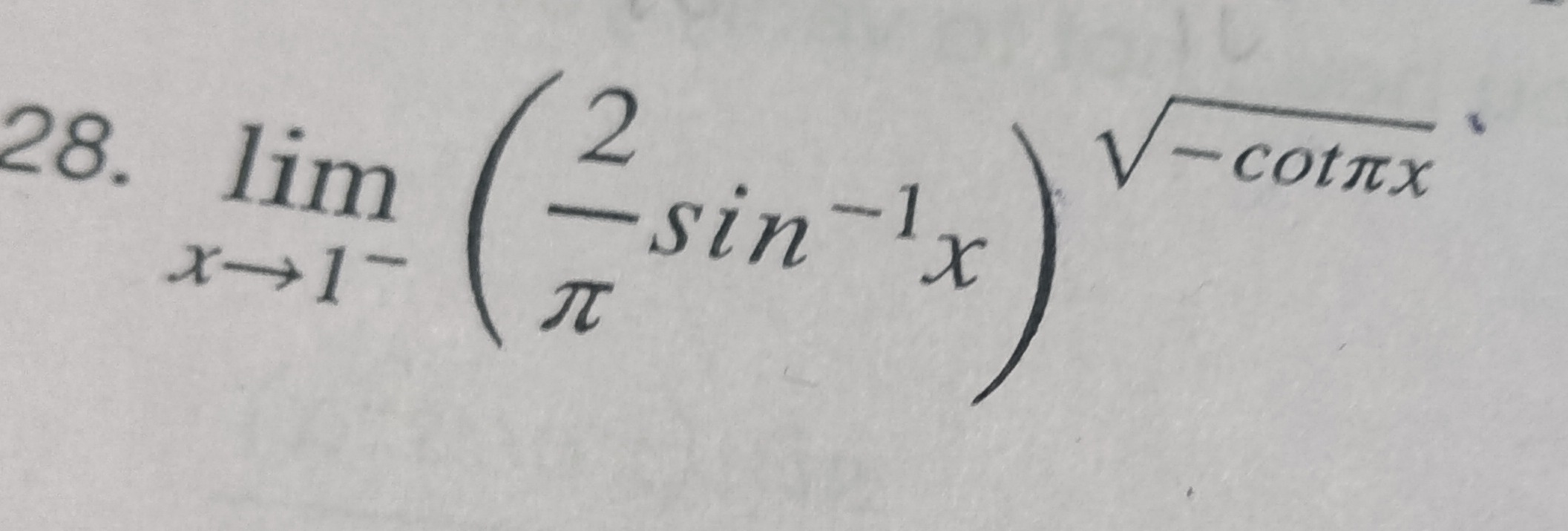
e−22/π3/2e^{-2\sqrt{2}/\pi^{3/2}}

Explanation

Solution

The limit is of the form 1∞1^\infty. We use the property that if lim⁡x→af(x)g(x)\lim_{x \to a} f(x)^{g(x)} is of the form 1∞1^\infty, then the limit is elim⁡x→ag(x)(f(x)−1)e^{\lim_{x \to a} g(x)(f(x)-1)}.

Let L=lim⁡x→1−(2πsin−1x)−cotπxL = \lim_{x\to 1^-} \left( \frac{2}{\pi}sin^{-1}x \right)^{\sqrt{-cot\pi x}}. Here, f(x)=2πsin−1xf(x) = \frac{2}{\pi}sin^{-1}x and g(x)=−cotπxg(x) = \sqrt{-cot\pi x}. As x→1−x \to 1^-, f(x)→2πsin−1(1)=2π⋅π2=1f(x) \to \frac{2}{\pi}sin^{-1}(1) = \frac{2}{\pi} \cdot \frac{\pi}{2} = 1. g(x)→−cot(π)=∞=∞g(x) \to \sqrt{-cot(\pi)} = \sqrt{\infty} = \infty. (As x→1−x \to 1^-, πx→π−\pi x \to \pi^-, so cot(πx)→−∞cot(\pi x) \to -\infty, making −cot(πx)→∞-cot(\pi x) \to \infty).

So, L=eKL = e^K, where K=lim⁡x→1−−cotπx(2πsin−1x−1)K = \lim_{x\to 1^-} \sqrt{-cot\pi x} \left( \frac{2}{\pi}sin^{-1}x - 1 \right).

To evaluate KK, let x=1−hx = 1 - h where h→0+h \to 0^+.

  1. Evaluate −cotπx\sqrt{-cot\pi x}: −cotπx=−cot(π(1−h))=−cot(π−πh)=−(−cot(πh))=cot(πh)\sqrt{-cot\pi x} = \sqrt{-cot(\pi(1-h))} = \sqrt{-cot(\pi - \pi h)} = \sqrt{-(-cot(\pi h))} = \sqrt{cot(\pi h)}. As h→0+h \to 0^+, πh→0+\pi h \to 0^+. We know that for small θ\theta, cot(θ)≈1θcot(\theta) \approx \frac{1}{\theta}. So, cot(πh)≈1πhcot(\pi h) \approx \frac{1}{\pi h}. Therefore, −cotπx≈1πh\sqrt{-cot\pi x} \approx \sqrt{\frac{1}{\pi h}}.

  2. Evaluate 2πsin−1x−1\frac{2}{\pi}sin^{-1}x - 1: Let sin−1x=π2−θsin^{-1}x = \frac{\pi}{2} - \theta. As x→1−x \to 1^-, θ→0+\theta \to 0^+. Then x=sin(π2−θ)=cos(θ)x = sin(\frac{\pi}{2} - \theta) = cos(\theta). Since x=1−hx = 1-h, we have 1−h=cos(θ)1-h = cos(\theta). For small θ\theta, cos(θ)≈1−θ22cos(\theta) \approx 1 - \frac{\theta^2}{2}. So, 1−h≈1−θ221-h \approx 1 - \frac{\theta^2}{2}, which implies h≈θ22h \approx \frac{\theta^2}{2}, or θ≈2h\theta \approx \sqrt{2h}. Now, substitute sin−1x=π2−θsin^{-1}x = \frac{\pi}{2} - \theta into the expression: 2πsin−1x−1=2π(π2−θ)−1=1−2θπ−1=−2θπ\frac{2}{\pi}sin^{-1}x - 1 = \frac{2}{\pi}\left(\frac{\pi}{2} - \theta\right) - 1 = 1 - \frac{2\theta}{\pi} - 1 = -\frac{2\theta}{\pi}. Using θ≈2h\theta \approx \sqrt{2h}, we get: 2πsin−1x−1≈−22hπ\frac{2}{\pi}sin^{-1}x - 1 \approx -\frac{2\sqrt{2h}}{\pi}.

  3. Calculate K: K=lim⁡h→0+(1πh)(−22hπ)K = \lim_{h\to 0^+} \left( \sqrt{\frac{1}{\pi h}} \right) \left( -\frac{2\sqrt{2h}}{\pi} \right) K=lim⁡h→0+(1πh)(−22hπ)K = \lim_{h\to 0^+} \left( \frac{1}{\sqrt{\pi}\sqrt{h}} \right) \left( -\frac{2\sqrt{2}\sqrt{h}}{\pi} \right) K=lim⁡h→0+−22ππK = \lim_{h\to 0^+} -\frac{2\sqrt{2}}{\pi\sqrt{\pi}} K=−22π3/2K = -\frac{2\sqrt{2}}{\pi^{3/2}}

Finally, the limit L=eKL = e^K. L=e−22/π3/2L = e^{-2\sqrt{2}/\pi^{3/2}}.