Question

In the shown figure, the heavy block of mass 2 kg rests on the horizontal surface and the lighter block of mass 1 kg is dropped from a height of 0.9 m. At the instant the string gets taut, find the upward speed (in m/s) of the heavy block.

Answer 1

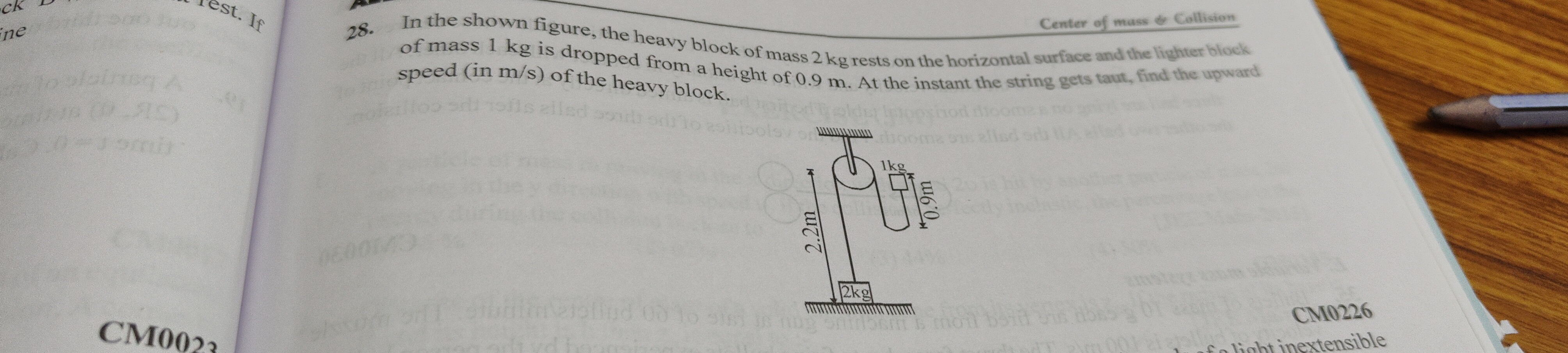
√2

Answer 2

The problem involves two stages:

1. The free fall of the lighter block until the string becomes taut.
2. The impulsive interaction when the string becomes taut, causing both blocks to move.

Stage 1: Free fall of the lighter block

• Mass of lighter block, $m = 1$ kg.
• Height dropped, $h = 0.9$ m.
• Initial velocity of lighter block, $u_m = 0$.
• We assume acceleration due to gravity, $g = 10 \text{ m/s}^2$.

Using the kinematic equation $v^2 = u^2 + 2as$, the speed of the lighter block ($v_m$) just before the string gets taut is: $v_m^2 = u_m^2 + 2gh$ $v_m^2 = 0^2 + 2 \times 10 \times 0.9$ $v_m^2 = 18$ $v_m = \sqrt{18} = 3\sqrt{2} \text{ m/s}$ (downwards).

Stage 2: Impulsive interaction when the string gets taut

• Mass of heavy block, $M = 2$ kg.
• Initial velocity of heavy block, $u_M = 0$ (it rests on the surface).
• When the string becomes taut, it's an impulsive event. During this very short time interval, external forces like gravity and normal force are negligible compared to the impulsive tension force in the string.
• Let $V$ be the common speed of both blocks immediately after the string becomes taut. Since the string is inextensible, if the heavy block moves up with speed $V$, the lighter block must move down with speed $V$.

We apply the impulse-momentum theorem to each block:

• For the lighter block ($m$): Initial momentum (downwards) $= m v_m$. Final momentum (downwards) $= m V$. The impulse acting on the lighter block is due to tension, which acts upwards. Let the magnitude of the impulse be $J$. Change in momentum = Final momentum - Initial momentum $m V - m v_m = -J$ (taking downwards as positive, so upward impulse is negative) -- (Equation 1)

• For the heavy block ($M$): Initial momentum (upwards) $= M u_M = 0$. Final momentum (upwards) $= M V$. The impulse acting on the heavy block is due to tension, which acts upwards. The magnitude of this impulse is also $J$ (since it's the same string). Change in momentum = Final momentum - Initial momentum $M V - 0 = J$ (taking upwards as positive) -- (Equation 2)

Now, substitute $J = MV$ from Equation 2 into Equation 1: $m V - m v_m = - (M V)$ $m V - m v_m = - M V$ Rearrange the terms to solve for $V$: $M V + m V = m v_m$ $V(M + m) = m v_m$ $V = \frac{m v_m}{M + m}$

Substitute the known values: $m = 1$ kg $M = 2$ kg $v_m = 3\sqrt{2}$ m/s

$V = \frac{1 \times 3\sqrt{2}}{2 + 1}$ $V = \frac{3\sqrt{2}}{3}$ $V = \sqrt{2} \text{ m/s}$

The upward speed of the heavy block is $\sqrt{2}$ m/s.

The final answer is $\boxed{\sqrt{2}}$.

Explanation of the solution:

1. Calculate the speed of the 1kg block ($m$) just before the string tautens using free-fall kinematics: $v_m = \sqrt{2gh} = \sqrt{2 \times 10 \times 0.9} = 3\sqrt{2} \text{ m/s}$.
2. During the impulsive event when the string tautens, apply the impulse-momentum theorem to each block.
3. For the 1kg block: $m(V - v_m) = -J$, where $J$ is the impulse magnitude and $V$ is the final common speed.
4. For the 2kg block ($M$): $MV - 0 = J$.
5. Combine these equations: $m(V - v_m) = -MV$.
6. Solve for $V$: $V(M+m) = mv_m \implies V = \frac{mv_m}{M+m}$.
7. Substitute values: $V = \frac{1 \times 3\sqrt{2}}{2+1} = \sqrt{2} \text{ m/s}$.

Answer: $\sqrt{2}$