Solveeit Logo
Login

Question

Question: 28. If $y = \tan^{-1} \sqrt{\frac{1 + \cos x}{1 - \cos x}}$, then $\frac{dy}{dx} =$...

  1. If y=tan⁡−11+cos⁡x1−cos⁡xy = \tan^{-1} \sqrt{\frac{1 + \cos x}{1 - \cos x}}, then dydx=\frac{dy}{dx} =
A

32\frac{3}{2}

B

0

C

1

D

−12-\frac{1}{2}

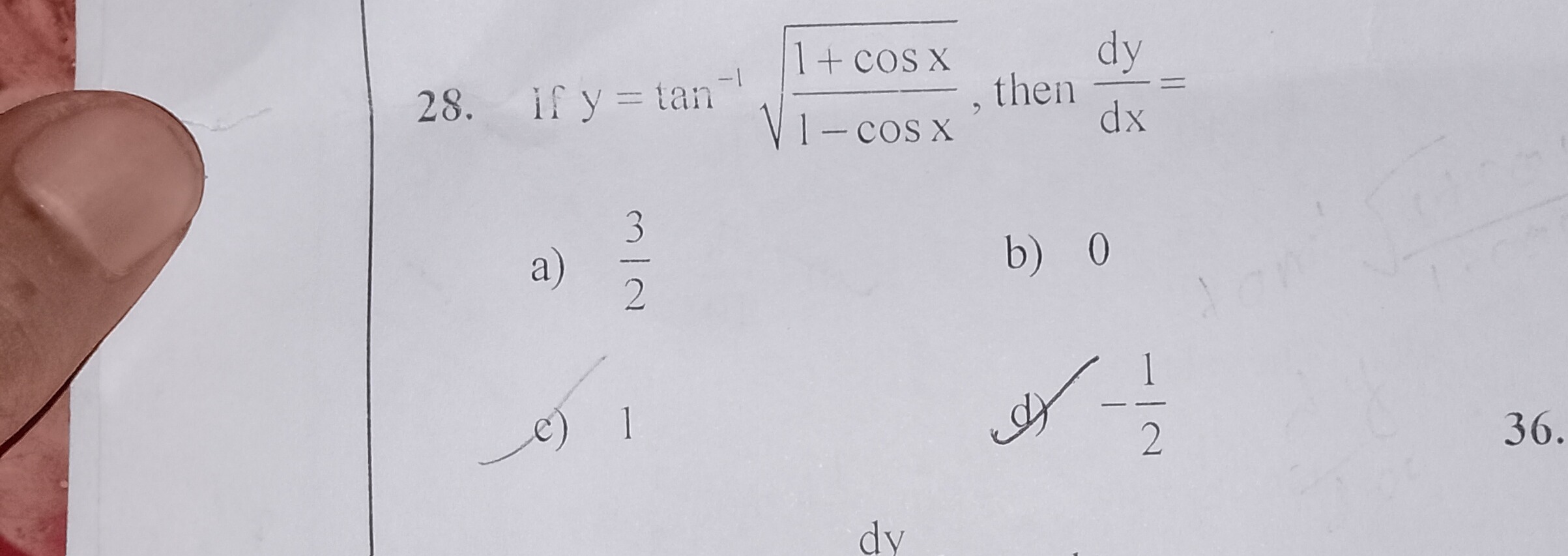
Answer

-\frac{1}{2}

Explanation

Solution

  1. Simplify the expression:

    1+cos⁡x1−cos⁡x=cot⁡x2(using half-angle identities)\sqrt{\frac{1+\cos x}{1-\cos x}} = \cot\frac{x}{2} \quad \text{(using half-angle identities)}

    Thus,

    y=tan⁡−1(cot⁡x2)=tan⁡−1(tan⁡(π2−x2))y = \tan^{-1}\left(\cot\frac{x}{2}\right) = \tan^{-1}\left(\tan\left(\frac{\pi}{2} - \frac{x}{2}\right)\right)

    which implies

    y=π2−x2.y = \frac{\pi}{2} - \frac{x}{2}.

  2. Differentiate with respect to xx:

    dydx=−12.\frac{dy}{dx} = -\frac{1}{2}.