Question
Question: If $\sin 2\theta + \sin 2\phi = \frac{1}{2}$ and $\cos 2\theta + \cos 2\phi = \frac{3}{2}$, $\cos^2...
If sin2θ+sin2ϕ=21 and cos2θ+cos2ϕ=23,
cos2(θ−ϕ)=
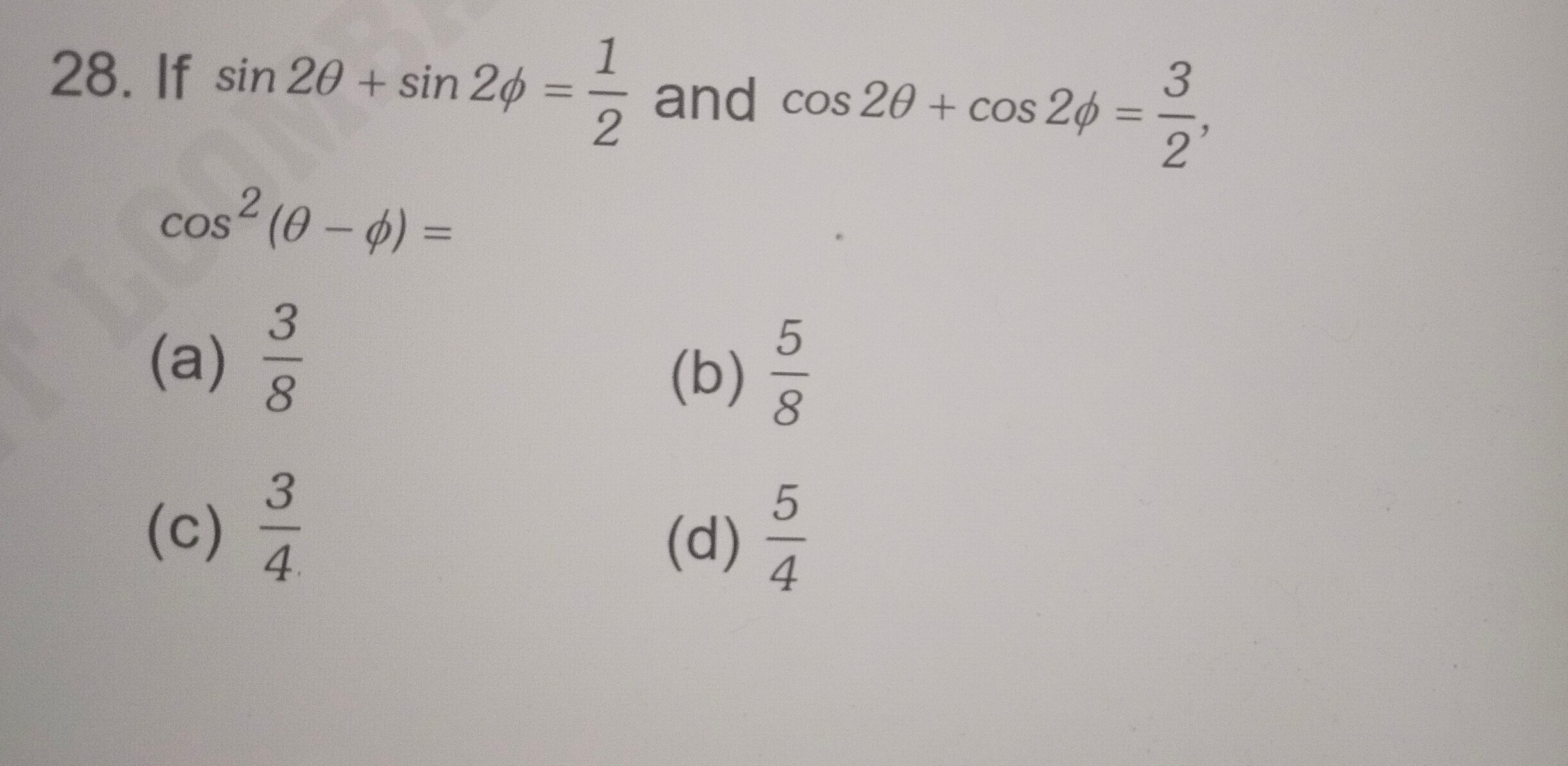
A
83
B
85
C
43
D
45
Answer
85
Explanation
Solution
We are given:
- sin2θ+sin2ϕ=21
- cos2θ+cos2ϕ=23
Using sum-to-product identities:
sinA+sinB=2sin(2A+B)cos(2A−B)
cosA+cosB=2cos(2A+B)cos(2A−B)
Applying these identities:
2sin(θ+ϕ)cos(θ−ϕ)=21 (Equation 3)
2cos(θ+ϕ)cos(θ−ϕ)=23 (Equation 4)
Squaring both equations:
4sin2(θ+ϕ)cos2(θ−ϕ)=41 (Equation 5)
4cos2(θ+ϕ)cos2(θ−ϕ)=49 (Equation 6)
Adding Equation 5 and Equation 6:
4sin2(θ+ϕ)cos2(θ−ϕ)+4cos2(θ+ϕ)cos2(θ−ϕ)=41+49
Factoring:
4cos2(θ−ϕ)[sin2(θ+ϕ)+cos2(θ+ϕ)]=410
Using the identity sin2x+cos2x=1:
4cos2(θ−ϕ)=410
Solving for cos2(θ−ϕ):
cos2(θ−ϕ)=1610=85
