Solveeit Logo
Login

Question

Question: If $D(x) = \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ (x+1) & (x+1)^2 & (x+1)^3 \en...

If D(x)=∣x−1(x−1)2x3xx2(x+1)3(x+1)(x+1)2(x+1)3∣D(x) = \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ (x+1) & (x+1)^2 & (x+1)^3 \end{vmatrix} then the coefficient of x in D(x) is-

A

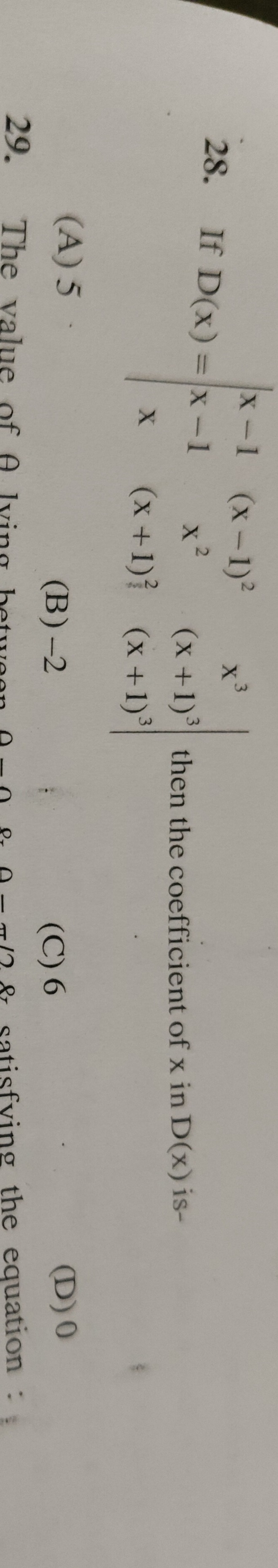
5

B

-2

C

6

D

0

Answer

5

Explanation

Solution

To find the coefficient of xx in D(x)D(x), we can use two methods:

  1. Expand the determinant and collect the terms with xx.
  2. Use the property that for a polynomial P(x)P(x), the coefficient of xx is P′(0)P'(0).

Method 1: Expansion and Collection of Terms

Given D(x)=∣x−1(x−1)2x3xx2(x+1)3(x+1)(x+1)2(x+1)3∣D(x) = \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ (x+1) & (x+1)^2 & (x+1)^3 \end{vmatrix}

Apply the row operation R3→R3−R2R_3 \rightarrow R_3 - R_2: D(x)=∣x−1(x−1)2x3xx2(x+1)3(x+1)−x(x+1)2−x2(x+1)3−(x+1)3∣D(x) = \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ (x+1)-x & (x+1)^2-x^2 & (x+1)^3-(x+1)^3 \end{vmatrix} D(x)=∣x−1(x−1)2x3xx2(x+1)31(x2+2x+1−x2)0∣D(x) = \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ 1 & (x^2+2x+1-x^2) & 0 \end{vmatrix} D(x)=∣x−1(x−1)2x3xx2(x+1)312x+10∣D(x) = \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ 1 & 2x+1 & 0 \end{vmatrix}

Now, expand the determinant along the third row (R3R_3): D(x)=1⋅∣(x−1)2x3x2(x+1)3∣−(2x+1)⋅∣x−1x3x(x+1)3∣+0⋅∣x−1(x−1)2xx2∣D(x) = 1 \cdot \begin{vmatrix} (x-1)^2 & x^3 \\ x^2 & (x+1)^3 \end{vmatrix} - (2x+1) \cdot \begin{vmatrix} x-1 & x^3 \\ x & (x+1)^3 \end{vmatrix} + 0 \cdot \begin{vmatrix} x-1 & (x-1)^2 \\ x & x^2 \end{vmatrix} D(x)=[(x−1)2(x+1)3−x2⋅x3]−(2x+1)[(x−1)(x+1)3−x⋅x3]D(x) = [(x-1)^2 (x+1)^3 - x^2 \cdot x^3] - (2x+1) [(x-1)(x+1)^3 - x \cdot x^3] D(x)=[(x−1)2(x+1)3−x5]−(2x+1)[(x−1)(x+1)3−x4]D(x) = [(x-1)^2 (x+1)^3 - x^5] - (2x+1) [(x-1)(x+1)^3 - x^4]

Let's find the coefficient of xx in each part:

Part 1: (x−1)2(x+1)3−x5(x-1)^2 (x+1)^3 - x^5 (x−1)2=x2−2x+1(x-1)^2 = x^2 - 2x + 1 (x+1)3=x3+3x2+3x+1(x+1)^3 = x^3 + 3x^2 + 3x + 1 The product (x−1)2(x+1)3=(x2−2x+1)(x3+3x2+3x+1)(x-1)^2 (x+1)^3 = (x^2 - 2x + 1)(x^3 + 3x^2 + 3x + 1). To find the coefficient of xx, we multiply terms whose powers sum to 1: (1)⋅(3x)+(−2x)⋅(1)=3x−2x=x(1) \cdot (3x) + (-2x) \cdot (1) = 3x - 2x = x. So, the coefficient of xx in (x−1)2(x+1)3(x-1)^2 (x+1)^3 is 11. The term −x5-x^5 does not contribute to the coefficient of xx. Contribution from Part 1 to coefficient of xx is 11.

Part 2: −(2x+1)[(x−1)(x+1)3−x4]-(2x+1) [(x-1)(x+1)^3 - x^4] Let A(x)=(x−1)(x+1)3−x4A(x) = (x-1)(x+1)^3 - x^4. First, find the terms up to xx in A(x)A(x): (x−1)(x+1)3=(x−1)(x3+3x2+3x+1)(x-1)(x+1)^3 = (x-1)(x^3 + 3x^2 + 3x + 1) =x(x3+3x2+3x+1)−1(x3+3x2+3x+1)= x(x^3 + 3x^2 + 3x + 1) - 1(x^3 + 3x^2 + 3x + 1) =x4+3x3+3x2+x−x3−3x2−3x−1= x^4 + 3x^3 + 3x^2 + x - x^3 - 3x^2 - 3x - 1 =x4+2x3−2x−1= x^4 + 2x^3 - 2x - 1 So, A(x)=(x4+2x3−2x−1)−x4=2x3−2x−1A(x) = (x^4 + 2x^3 - 2x - 1) - x^4 = 2x^3 - 2x - 1. Now, we need the coefficient of xx in −(2x+1)A(x)=−(2x+1)(2x3−2x−1)-(2x+1)A(x) = -(2x+1)(2x^3 - 2x - 1). Consider only terms contributing to xx: −((2x)(−1)+(1)(−2x))-( (2x)(-1) + (1)(-2x) ) =−(−2x−2x)=−(−4x)=4x= -(-2x - 2x) = -(-4x) = 4x. Contribution from Part 2 to coefficient of xx is 44.

Total coefficient of xx in D(x)D(x) is the sum of contributions from Part 1 and Part 2: 1+4=51 + 4 = 5.

Method 2: Using Derivatives

The coefficient of xx in a polynomial P(x)P(x) is P′(0)P'(0). We need to find D′(0)D'(0). The derivative of a determinant is the sum of determinants where one row/column is differentiated at a time. D′(x)=∣ddx(x−1)ddx(x−1)2ddx(x3)xx2(x+1)3(x+1)(x+1)2(x+1)3∣+∣x−1(x−1)2x3ddx(x)ddx(x2)ddx(x+1)3(x+1)(x+1)2(x+1)3∣+∣x−1(x−1)2x3xx2(x+1)3ddx(x+1)ddx(x+1)2ddx(x+1)3∣D'(x) = \begin{vmatrix} \frac{d}{dx}(x-1) & \frac{d}{dx}(x-1)^2 & \frac{d}{dx}(x^3) \\ x & x^2 & (x+1)^3 \\ (x+1) & (x+1)^2 & (x+1)^3 \end{vmatrix} + \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ \frac{d}{dx}(x) & \frac{d}{dx}(x^2) & \frac{d}{dx}(x+1)^3 \\ (x+1) & (x+1)^2 & (x+1)^3 \end{vmatrix} + \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ \frac{d}{dx}(x+1) & \frac{d}{dx}(x+1)^2 & \frac{d}{dx}(x+1)^3 \end{vmatrix}

D′(x)=∣12(x−1)3x2xx2(x+1)3(x+1)(x+1)2(x+1)3∣+∣x−1(x−1)2x312x3(x+1)2(x+1)(x+1)2(x+1)3∣+∣x−1(x−1)2x3xx2(x+1)312(x+1)3(x+1)2∣D'(x) = \begin{vmatrix} 1 & 2(x-1) & 3x^2 \\ x & x^2 & (x+1)^3 \\ (x+1) & (x+1)^2 & (x+1)^3 \end{vmatrix} + \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ 1 & 2x & 3(x+1)^2 \\ (x+1) & (x+1)^2 & (x+1)^3 \end{vmatrix} + \begin{vmatrix} x-1 & (x-1)^2 & x^3 \\ x & x^2 & (x+1)^3 \\ 1 & 2(x+1) & 3(x+1)^2 \end{vmatrix}

Now, substitute x=0x=0 into D′(x)D'(x): D′(0)=∣12(−1)3(0)2002(0+1)3(0+1)(0+1)2(0+1)3∣+∣(0−1)(0−1)20312(0)3(0+1)2(0+1)(0+1)2(0+1)3∣+∣(0−1)(0−1)203002(0+1)312(0+1)3(0+1)2∣D'(0) = \begin{vmatrix} 1 & 2(-1) & 3(0)^2 \\ 0 & 0^2 & (0+1)^3 \\ (0+1) & (0+1)^2 & (0+1)^3 \end{vmatrix} + \begin{vmatrix} (0-1) & (0-1)^2 & 0^3 \\ 1 & 2(0) & 3(0+1)^2 \\ (0+1) & (0+1)^2 & (0+1)^3 \end{vmatrix} + \begin{vmatrix} (0-1) & (0-1)^2 & 0^3 \\ 0 & 0^2 & (0+1)^3 \\ 1 & 2(0+1) & 3(0+1)^2 \end{vmatrix}

D′(0)=∣1−20001111∣+∣−110103111∣+∣−110001123∣D'(0) = \begin{vmatrix} 1 & -2 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \end{vmatrix} + \begin{vmatrix} -1 & 1 & 0 \\ 1 & 0 & 3 \\ 1 & 1 & 1 \end{vmatrix} + \begin{vmatrix} -1 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 2 & 3 \end{vmatrix}

Calculate each determinant:

  1. ∣1−20001111∣=1(0⋅1−1⋅1)−(−2)(0⋅1−1⋅1)+0=1(−1)+2(−1)=−1−2=−3\begin{vmatrix} 1 & -2 & 0 \\ 0 & 0 & 1 \\ 1 & 1 & 1 \end{vmatrix} = 1(0 \cdot 1 - 1 \cdot 1) - (-2)(0 \cdot 1 - 1 \cdot 1) + 0 = 1(-1) + 2(-1) = -1 - 2 = -3.
  2. ∣−110103111∣=−1(0⋅1−3⋅1)−1(1⋅1−3⋅1)+0=−1(−3)−1(1−3)=3−1(−2)=3+2=5\begin{vmatrix} -1 & 1 & 0 \\ 1 & 0 & 3 \\ 1 & 1 & 1 \end{vmatrix} = -1(0 \cdot 1 - 3 \cdot 1) - 1(1 \cdot 1 - 3 \cdot 1) + 0 = -1(-3) - 1(1-3) = 3 - 1(-2) = 3+2 = 5.
  3. ∣−110001123∣=−1(0⋅3−1⋅2)−1(0⋅3−1⋅1)+0=−1(−2)−1(−1)=2+1=3\begin{vmatrix} -1 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 2 & 3 \end{vmatrix} = -1(0 \cdot 3 - 1 \cdot 2) - 1(0 \cdot 3 - 1 \cdot 1) + 0 = -1(-2) - 1(-1) = 2+1 = 3.

Summing these values: D′(0)=−3+5+3=5D'(0) = -3 + 5 + 3 = 5.

Both methods yield the same result.

The final answer is 5\boxed{\text{5}}.