Question

Find a point on the curve $x^2+2y^2=6$ whose distance from the line x+y=7, is as small as possible.

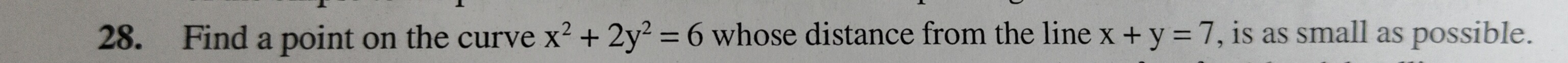
• A. The point is (2, 1).
• B. The point is (-2, -1).
• C. The point is (1, 2).
• D. The point is (-1, -2).

Answer 1

Answer: (A)

The point is (2, 1).

Answer 2

The distance from a point $(x, y)$ on the ellipse $x^2+2y^2=6$ to the line $x+y-7=0$ is given by $D = \frac{|x+y-7|}{\sqrt{2}}$. To minimize $D$, the tangent to the ellipse must be parallel to the line $x+y=7$. The slope of the line is $-1$. Implicitly differentiating the ellipse equation gives $\frac{dy}{dx} = -\frac{x}{2y}$. Setting $-\frac{x}{2y} = -1$ yields $x=2y$. Substituting this into the ellipse equation: $(2y)^2 + 2y^2 = 6 \implies 6y^2 = 6 \implies y = \pm 1$. The points are $(2, 1)$ and $(-2, -1)$. Evaluating the distance at these points, $(2, 1)$ yields a smaller distance than $(-2, -1)$.