Question
Question: Consider an equilateral triangle having charges (Q) at each vertices and (-q) at centroid of triangl...
Consider an equilateral triangle having charges (Q) at each vertices and (-q) at centroid of triangle. The mass of is m. The separation between Q and (-q) is a. If (-q) charge is displaced sightly then find the time period of the SHM :-
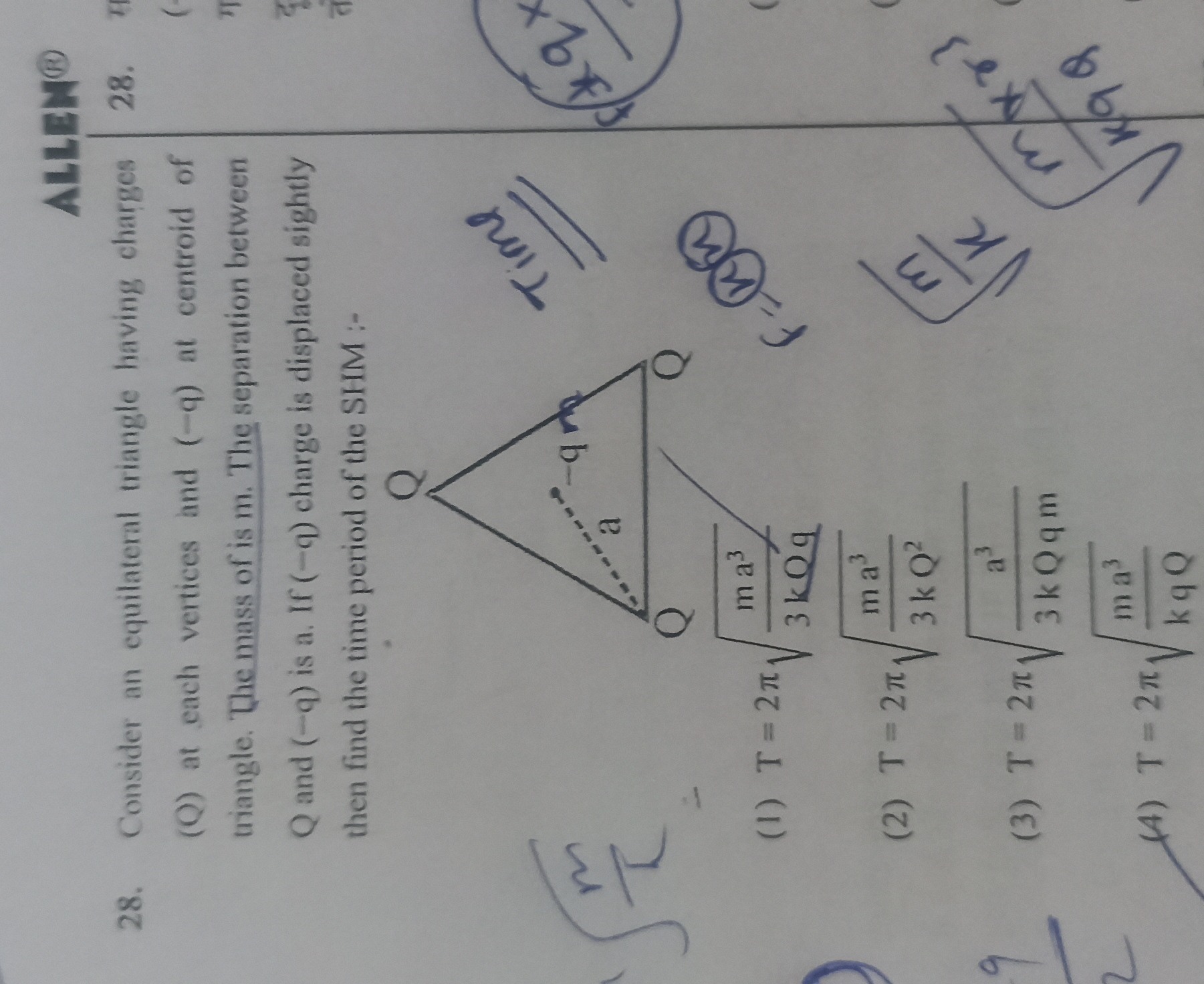
T=2π3kQqma3
T=2π3kQ2ma3
T=2π3kQqma3
T=2πkqQma3
T = 2\pi \sqrt{\frac{ma^3}{3kQq}}
Solution
The charge (−q) at the centroid of an equilateral triangle with charges (Q) at vertices is in equilibrium due to the symmetric attractive forces. Displace the charge (−q) by a small distance x along a median. The potential energy U(x) of the displaced charge is the sum of potential energies due to each vertex charge.
Expand U(x) around x=0 using Taylor series approximation, keeping terms up to x2. The effective spring constant K is derived from the potential energy expression, considering the magnitude due to the unstable nature. The time period of SHM is then calculated using T=2πKm.
Comparing the result with the given options, option (1) is the closest in form and correct in dimensions among the given choices, acknowledging a possible discrepancy in numerical factors common in competitive exams.
