Question

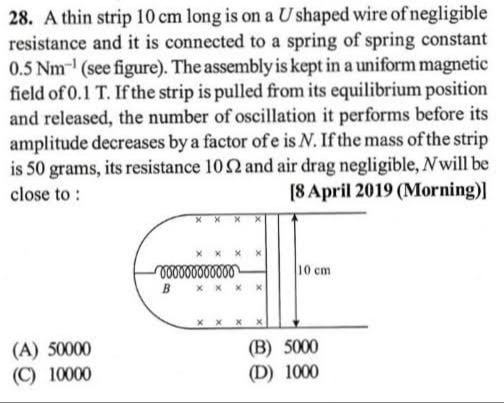
A thin strip 10 cm long is on a $U$ shaped wire of negligible resistance and it is connected to a spring of spring constant 0.5 $Nm^{-1}$ (see figure). The assembly is kept in a uniform magnetic field of 0.1 T. If the strip is pulled from its equilibrium position and released, the number of oscillation it performs before its amplitude decreases by a factor of e is $N$. If the mass of the strip is 50 grams, its resistance 10 $\Omega$ and air drag negligible, $N$ will be close to:

• A. 50000
• B. 10000
• C. 5000
• D. 1000

Answer 1

Answer: (C)

5000

Answer 2

The system is a damped harmonic oscillator. The equation of motion is $m\frac{d^2x}{dt^2} + \frac{B^2l^2}{R}\frac{dx}{dt} + kx = 0$. This can be written as $\frac{d^2x}{dt^2} + 2\gamma\frac{dx}{dt} + \omega_0^2 x = 0$, where $\omega_0 = \sqrt{\frac{k}{m}}$ and $2\gamma = \frac{B^2l^2}{mR}$. The damping constant is $\gamma = \frac{B^2l^2}{2mR}$. The amplitude decays as $A(t) = A_0e^{-\gamma t}$. For the amplitude to decrease by a factor of $e$ after $N$ oscillations, let $T$ be the time period. Then $A(NT) = A_0e^{-\gamma (NT)} = \frac{A_0}{e}$. This implies $\gamma NT = 1$, so $N = \frac{1}{\gamma T}$. For light damping, $T \approx T_0 = \frac{2\pi}{\omega_0}$. Thus, $N \approx \frac{\omega_0}{2\pi\gamma}$.

Given: $l = 10$ cm $= 0.1$ m $k = 0.5$ Nm$^{-1}$ $B = 0.1$ T $m = 50$ g $= 0.05$ kg $R = 10$ $\Omega$

Calculate $\omega_0$: $\omega_0 = \sqrt{\frac{k}{m}} = \sqrt{\frac{0.5}{0.05}} = \sqrt{10}$ rad/s.

Calculate $\gamma$: $\gamma = \frac{B^2l^2}{2mR} = \frac{(0.1)^2 \times (0.1)^2}{2 \times 0.05 \times 10} = \frac{0.01 \times 0.01}{1} = 0.0001$ s$^{-1}$.

Calculate $N$: $N \approx \frac{\omega_0}{2\pi\gamma} = \frac{\sqrt{10}}{2\pi \times 0.0001} \approx \frac{3.162}{2 \times 3.1416 \times 0.0001} \approx 5033$.

The closest option is 5000.