Question

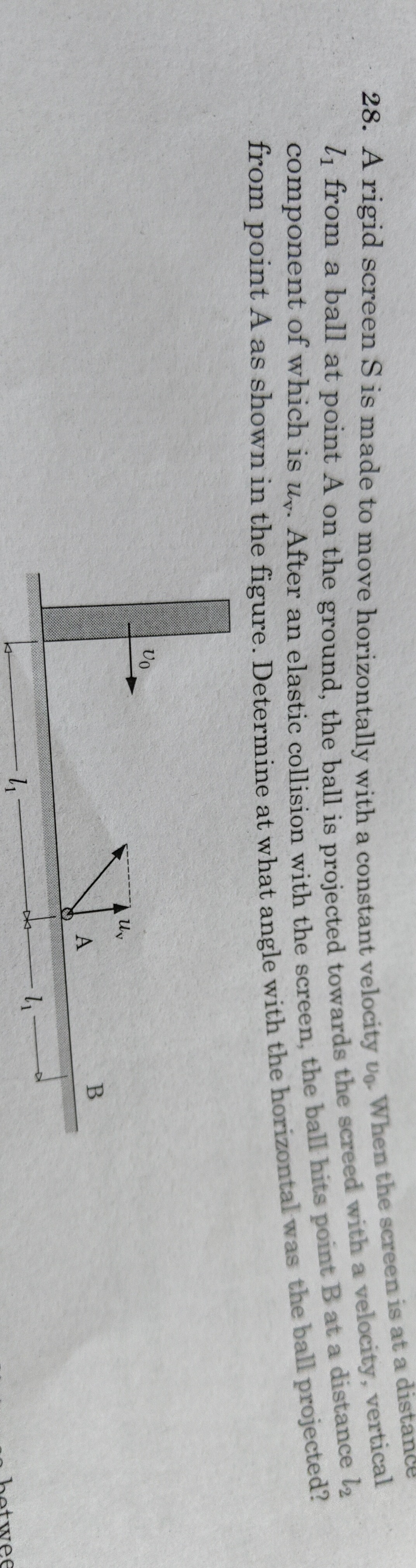
A rigid screen S is made to move horizontally with a constant velocity $v_0$. When the screen is at a distance $l_1$ from a ball at point A on the ground, the ball is projected towards the screed with a velocity, vertical component of which is $u_v$. After an elastic collision with the screen, the ball hits point B at a distance $l_2$ from point A as shown in the figure. Determine at what angle with the horizontal was the ball projected?

Answer 1

$\alpha = \arctan\left(\frac{2 u_v^2}{g(2l_1 - l_2) - 4u_v v_0}\right)$

Answer 2

The problem describes a projectile motion followed by an elastic collision with a moving screen. We need to find the initial projection angle of the ball.

Let the initial horizontal component of the ball's velocity be $u_h$ and the initial vertical component be $u_v$. The screen moves horizontally with a constant velocity $v_0$ towards the ball (from right to left in the diagram). Let's define the positive x-direction as from A towards the initial position of the screen.

1. Motion until collision:

• The ball is projected from point A (origin, $x=0$). Its horizontal position at time $t$ is $x_{ball}(t) = u_h t$.
• The screen is initially at a distance $l_1$ from A, so its initial position is $x_{screen}(0) = l_1$. Since it moves towards A with velocity $v_0$, its position at time $t$ is $x_{screen}(t) = l_1 - v_0 t$.
• Collision occurs at time $t_1$ when their positions are equal: $u_h t_1 = l_1 - v_0 t_1$ $(u_h + v_0) t_1 = l_1$ $t_1 = \frac{l_1}{u_h + v_0}$
• The horizontal position where the collision occurs is $x_C = u_h t_1 = \frac{u_h l_1}{u_h + v_0}$.

2. Elastic collision with the screen:

• The collision is elastic, and the screen is rigid and moves horizontally. This means the vertical component of the ball's velocity remains unchanged during the collision.
• Let the ball's horizontal velocity just before collision be $u_{1x} = u_h$.
• The screen's velocity is $v_S = -v_0$ (negative sign indicates motion towards A).
• Let the ball's horizontal velocity just after collision be $v_{2x}$.
• For an elastic collision, the relative speed of approach equals the relative speed of separation. Relative velocity of ball with respect to screen before collision: $u_{rel,i} = u_{1x} - v_S = u_h - (-v_0) = u_h + v_0$. Relative velocity of ball with respect to screen after collision: $u_{rel,f} = v_{2x} - v_S = v_{2x} - (-v_0) = v_{2x} + v_0$.
• Since the collision is elastic, $u_{rel,f} = -u_{rel,i}$: $v_{2x} + v_0 = -(u_h + v_0)$ $v_{2x} = -u_h - 2v_0$
• So, after collision, the ball's horizontal velocity is $-(u_h + 2v_0)$, meaning its speed is $(u_h + 2v_0)$ directed towards A (to the left).

3. Motion after collision:

• The ball starts from $x_C$ with horizontal velocity $v_{2x} = -(u_h + 2v_0)$ and lands at point B, which is at a distance $l_2$ from A. So, its final x-coordinate is $x_B = l_2$.
• Let $t_2$ be the time taken for the ball to travel from the collision point to point B. $x_B = x_C + v_{2x} t_2$ $l_2 = \frac{u_h l_1}{u_h + v_0} - (u_h + 2v_0) t_2$
• Solving for $t_2$: $(u_h + 2v_0) t_2 = \frac{u_h l_1}{u_h + v_0} - l_2$ $t_2 = \frac{1}{u_h + 2v_0} \left( \frac{u_h l_1}{u_h + v_0} - l_2 \right)$

4. Total time of flight:

• The ball is projected from the ground (A) and lands back on the ground (B). The total time of flight $T$ for a projectile motion from ground to ground is given by: $T = \frac{2 u_v}{g}$
• The total time of flight is also the sum of time before collision and time after collision: $T = t_1 + t_2$. $\frac{2 u_v}{g} = \frac{l_1}{u_h + v_0} + \frac{1}{u_h + 2v_0} \left( \frac{u_h l_1}{u_h + v_0} - l_2 \right)$
• Combine the terms on the right side by finding a common denominator: $\frac{2 u_v}{g} = \frac{l_1(u_h + 2v_0) + (u_h + v_0) \left( \frac{u_h l_1}{u_h + v_0} - l_2 \right)}{(u_h + v_0)(u_h + 2v_0)}$ $\frac{2 u_v}{g} = \frac{l_1 u_h + 2l_1 v_0 + u_h l_1 - l_2(u_h + v_0)}{(u_h + v_0)(u_h + 2v_0)}$ $\frac{2 u_v}{g} = \frac{2u_h l_1 + 2l_1 v_0 - l_2 u_h - l_2 v_0}{(u_h + v_0)(u_h + 2v_0)}$ $\frac{2 u_v}{g} = \frac{u_h(2l_1 - l_2) + v_0(2l_1 - l_2)}{(u_h + v_0)(u_h + 2v_0)}$ $\frac{2 u_v}{g} = \frac{(u_h + v_0)(2l_1 - l_2)}{(u_h + v_0)(u_h + 2v_0)}$
• Assuming $u_h + v_0 \neq 0$ (which is true as $u_h, v_0 > 0$), we can cancel the $(u_h + v_0)$ term: $\frac{2 u_v}{g} = \frac{2l_1 - l_2}{u_h + 2v_0}$

5. Determine the angle of projection:

• From the simplified equation, we can find $u_h$: $u_h + 2v_0 = \frac{g(2l_1 - l_2)}{2 u_v}$ $u_h = \frac{g(2l_1 - l_2)}{2 u_v} - 2v_0$
• Let $\alpha$ be the angle of projection with the horizontal. We know that $\tan\alpha = \frac{u_v}{u_h}$. $\tan\alpha = \frac{u_v}{\frac{g(2l_1 - l_2)}{2 u_v} - 2v_0}$ $\tan\alpha = \frac{u_v}{\frac{g(2l_1 - l_2) - 4u_v v_0}{2 u_v}}$ $\tan\alpha = \frac{2 u_v^2}{g(2l_1 - l_2) - 4u_v v_0}$

The angle of projection is $\alpha = \arctan\left(\frac{2 u_v^2}{g(2l_1 - l_2) - 4u_v v_0}\right)$.