Question
Question: A ray at a height h parallel to the principal axis is incident on a concave mirror of radius of curv...
A ray at a height h parallel to the principal axis is incident on a concave mirror of radius of curvature R.
h=2R, the value of x:
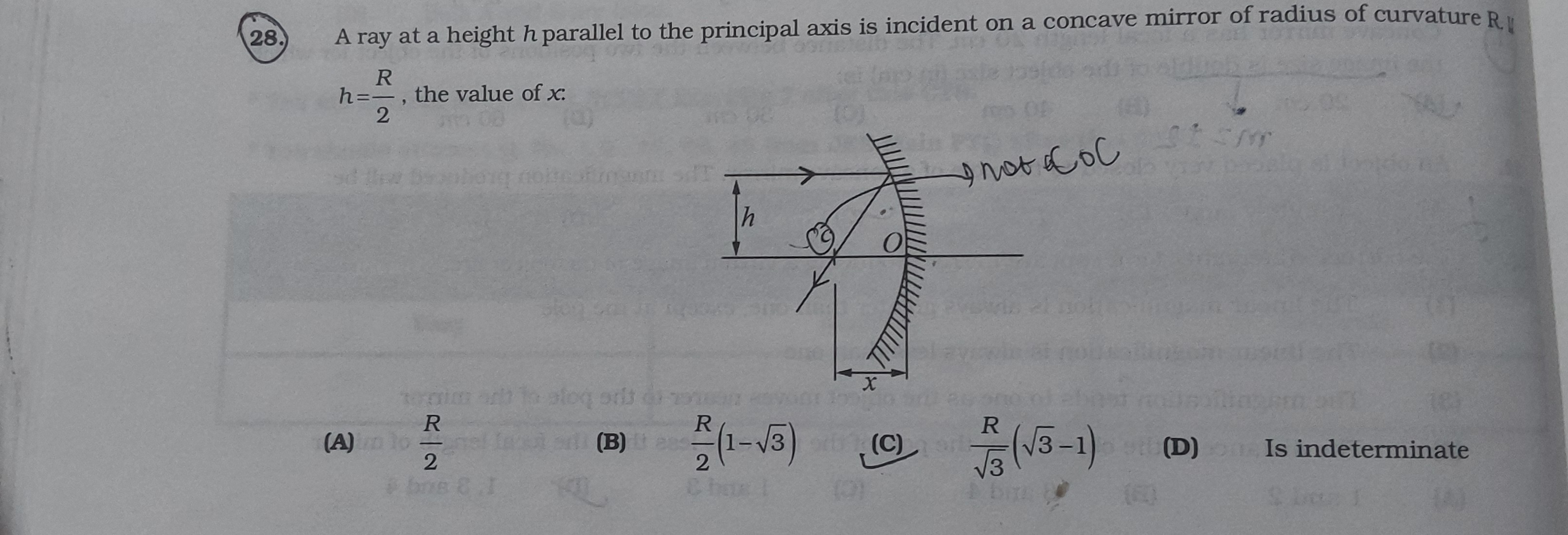
2R
2R(1−3)
3R(3−1)
Is indeterminate
3R(3−1)
Solution
Let's analyze the problem using the geometry of reflection.
-
Identify Key Points and Distances:
- Let O be the pole of the concave mirror. We place O at the origin (0,0) of a coordinate system.
- Let C be the center of curvature. For a concave mirror, C is at (R,0).
- Let A be the point on the mirror where the ray is incident. The ray is at a height h=R/2 and parallel to the principal axis. So, the y-coordinate of A is h=R/2. Let its x-coordinate be xA.
- The distance from A to C is equal to the radius of curvature R. Using the distance formula: (xA−R)2+(h−0)2=R2 (xA−R)2+h2=R2 Substitute h=R/2: (xA−R)2+(R/2)2=R2 (xA−R)2=R2−R2/4=3R2/4 xA−R=±3R2/4=±23R Since A is on the mirror surface to the left of the pole, xA must be positive. xA=R−23R=R(1−23).
- Let P be the projection of A onto the principal axis. The coordinates of P are (xA,0). So, OP=∣xA∣=R(1−23). And AP=h=R/2.
-
Determine the Angle of Incidence:
- Draw the normal to the mirror at point A. This normal passes through the center of curvature C.
- Let α be the angle between the normal CA and the principal axis.
- Consider the right-angled triangle formed by C, P, and A. CP=∣xA−R∣=∣R(1−23)−R∣=∣−23R∣=23R. CA=R. cosα=CACP=R23R=23. Therefore, α=30∘.
- The incident ray is parallel to the principal axis. The angle of incidence (i) is the angle between the incident ray and the normal. Since the incident ray is parallel to the principal axis, the angle between the incident ray and the normal CA is equal to α. So, i=α=30∘.
-
Determine the Path of the Reflected Ray:
- According to the law of reflection, the angle of reflection (r) equals the angle of incidence (i). So, r=i=30∘.
- The reflected ray makes an angle r=30∘ with the normal CA.
- The angle that the reflected ray makes with the principal axis (θ) can be found. The normal CA makes an angle α with the principal axis. The incident ray is parallel to the principal axis. The angle between the incident ray and the normal is α. The reflected ray is on the other side of the normal, making an angle α with it. Thus, the total angle the reflected ray makes with the principal axis is θ=α+α=2α. So, θ=2×30∘=60∘.
- The reflected ray passes through A and intersects the principal axis at a point F'. The distance OF' is 'x'.
- Consider the right-angled triangle formed by A, P, and F'. AP=h=R/2. PF′=AP/tanθ=h/tan(60∘). PF′=(R/2)/3=R/(23).
-
Calculate 'x':
-
The x-coordinate of P is xA=R(1−23). This is a positive value, meaning P is to the right of O.
-
The reflected ray intersects the principal axis at F'. The x-coordinate of F' is xF′=xA−PF′. xF′=R(1−23)−23R xF′=R(1−23−231) To simplify, multiply the last term by 3/3: 231=63. xF′=R(1−23−63) xF′=R(1−633−63) xF′=R(1−643)=R(1−323)
-
The distance 'x' shown in the diagram is the distance from the pole O to the intersection point F'. So, x=xF′. x=R(1−323). This can be rewritten as: x=R(1−323)=R(33−23).
-
Let's check the options. Option (C) is 3R(3−1)=R(1−31)=R(1−33).
So, the error was in the sign of PF′. We have xF′=xA−PF′. xF′=R(1−23)−23R. x=∣xF′∣. The correct result is x=R(1−33).
-
