Question

Simplify the expression:

$5^{5^x}\cdot 5^x$

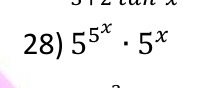
Answer 1

$5^{5^x+x}$

Answer 2

To simplify the expression $5^{5^x} \cdot 5^x$, we use the law of exponents which states that when multiplying powers with the same base, you add the exponents:

$a^m \cdot a^n = a^{m+n}$

In this expression:

• The base $a$ is $5$.
• The exponent $m$ for the first term is $5^x$.
• The exponent $n$ for the second term is $x$.

Applying the rule:

$5^{5^x} \cdot 5^x = 5^{(5^x + x)}$

The exponents $5^x$ and $x$ are distinct terms and cannot be combined further unless a specific value for $x$ is known. Therefore, the simplified form is $5^{5^x+x}$.