Question
Question: What is the magnetic field at O due to current in the infinite wire forming a loop as shown in the f...
What is the magnetic field at O due to current in the infinite wire forming a loop as shown in the following figure?
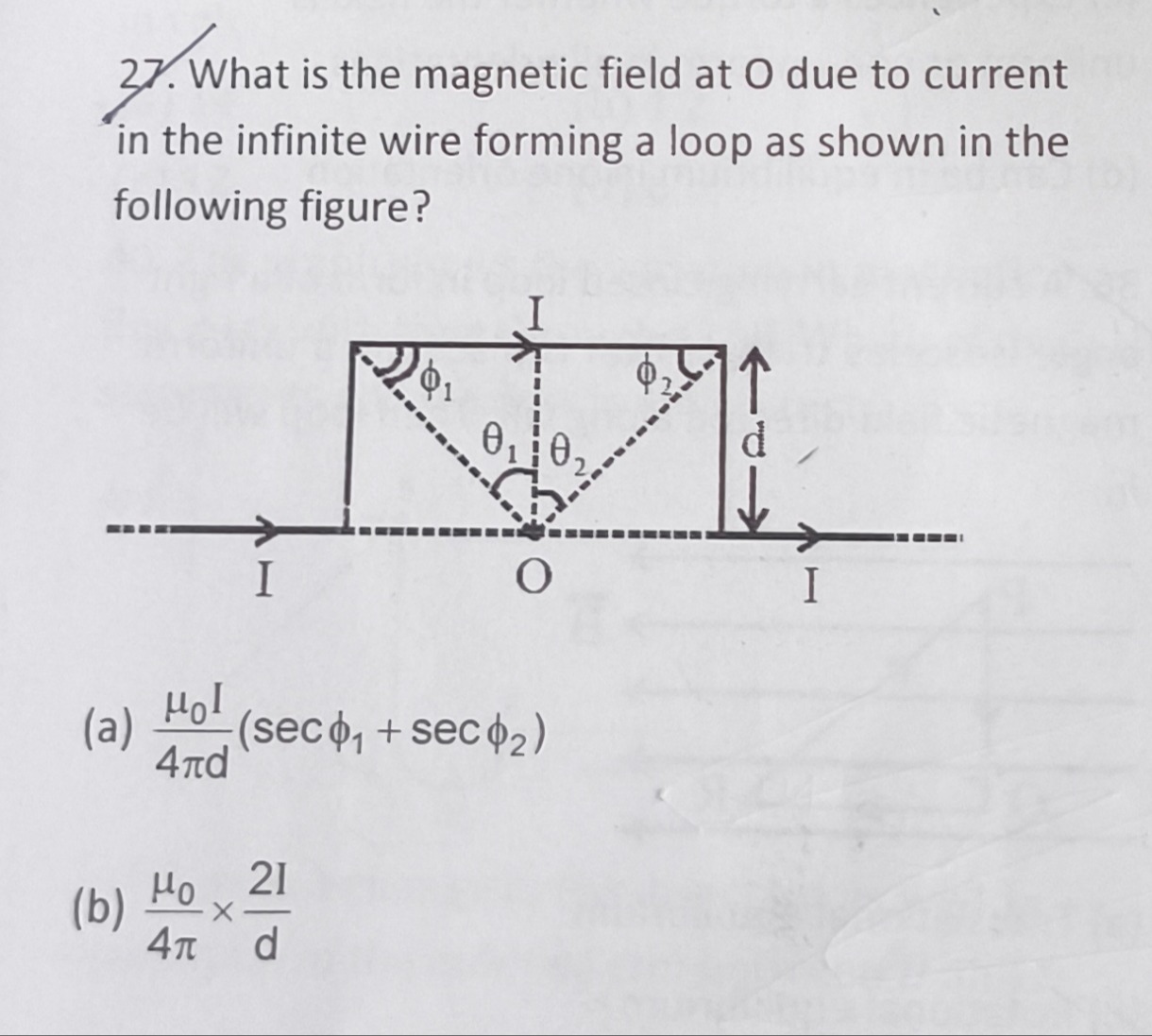
4πdμ0I(secϕ1+secϕ2)
4πμ0×d2I
(a)
Solution
The problem asks for the magnetic field at point O due to the current in the given wire configuration. The configuration consists of an infinite wire that forms a rectangular loop.
Given the options, it is highly probable that the question intends for the angles ϕ1 and ϕ2 in option (a) to be the angles θ1 and θ2 as defined in the diagram (angles at O from the vertical to the diagonal lines). And it also implies that only the vertical segments contribute to the field. This is a common simplification in some problems, or a mistake.
Magnetic field due to left vertical wire at O: B1=4πdμ0Isecθ1.
Magnetic field due to right vertical wire at O: B2=4πdμ0Isecθ2.
Both fields are directed out of the page.
Total field (under this assumption) B=B1+B2=4πdμ0I(secθ1+secθ2).
Replacing θ1,θ2 with ϕ1,ϕ2 as per the option format, we get option (a).
