Question

The sum $\sum_{k=1}^{\infty} \frac{6^k}{(3^k-2^k)(3^{k+1}-2^{k+1})}$ is equal to

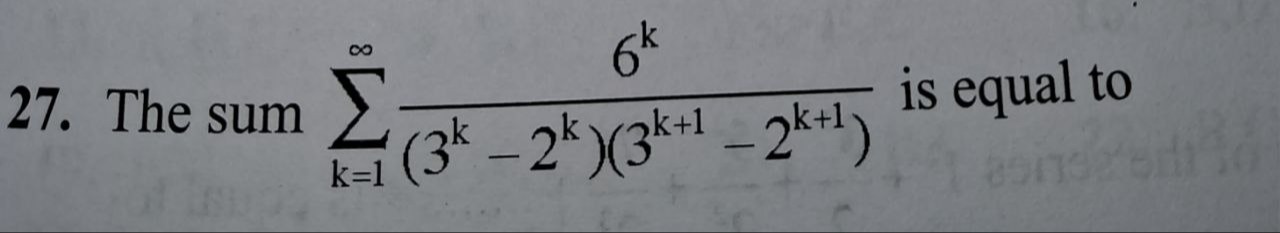
Answer 1

2

Answer 2

The general term $T_k = \frac{6^k}{(3^k-2^k)(3^{k+1}-2^{k+1})}$ is transformed by dividing the numerator and denominator by $3^k \cdot 3^{k+1}$. This leads to $T_k = \frac{1}{3} \frac{(2/3)^k}{(1-(2/3)^k)(1-(2/3)^{k+1})}$. By setting $x=2/3$, the term $\frac{x^k}{(1-x^k)(1-x^{k+1})}$ is expressed as a difference $\frac{1}{1-x} \left( \frac{1}{1-x^k} - \frac{1}{1-x^{k+1}} \right)$. Substituting $x=2/3$ back, $T_k$ simplifies to $f(k) - f(k+1)$ where $f(k) = \frac{1}{1-(2/3)^k}$. This creates a telescoping series. The sum is $f(1) - \lim_{N \to \infty} f(N+1)$. Evaluating $f(1)=3$ and $\lim_{N \to \infty} f(N+1)=1$, the sum is $3-1=2$.