Question
Question: $\lim_{x \to 1} \left( \frac{2024}{x^{2024}-1} - \frac{2022}{x^{2022}-1} \right)$...
limx→1(x2024−12024−x2022−12022)
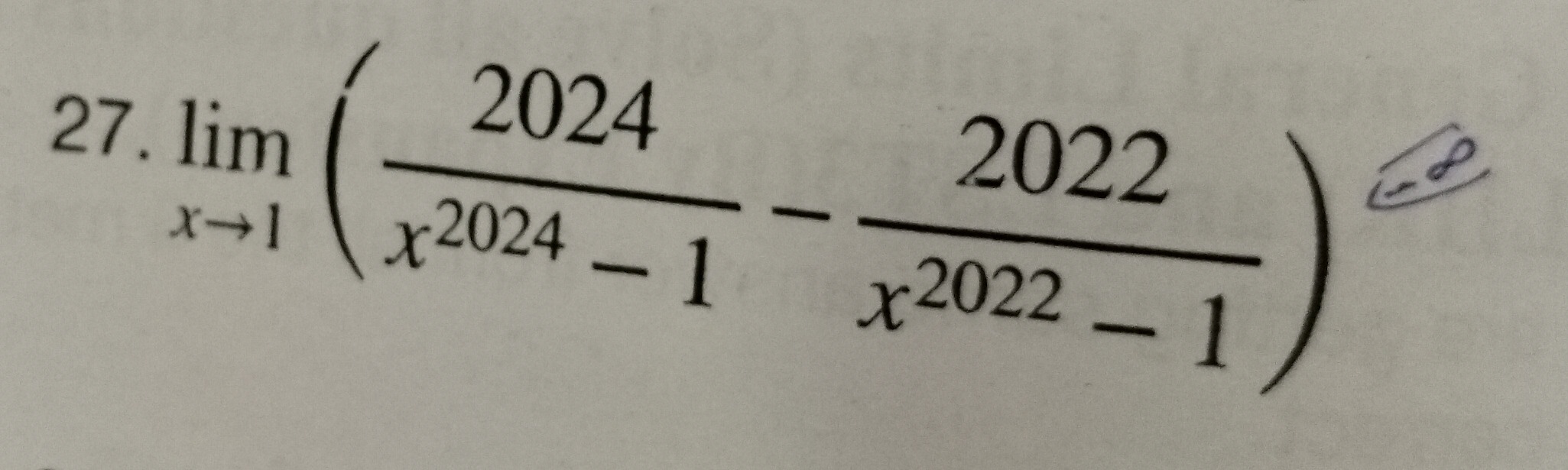
1
-1
0
The limit does not exist.
-1
Solution
To solve the limit limx→1(x2024−12024−x2022−12022), we first observe that as x→1, both denominators x2024−1 and x2022−1 approach 0. This results in an indeterminate form of type ∞−∞.
We combine the fractions: L=limx→1(x2024−1)(x2022−1)2024(x2022−1)−2022(x2024−1) Let the numerator be N(x)=2024(x2022−1)−2022(x2024−1)=2024x2022−2024−2022x2024+2022=−2022x2024+2024x2022−2. Let the denominator be D(x)=(x2024−1)(x2022−1).
As x→1, N(1)=−2022(1)2024+2024(1)2022−2=−2022+2024−2=0. And D(1)=(12024−1)(12022−1)=(1−1)(1−1)=0. This is an indeterminate form of type 00, so we can apply L'Hopital's Rule.
Let n1=2024 and n2=2022. The expression becomes: L=limx→1(xn1−1)(xn2−1)n1(xn2−1)−n2(xn1−1) Numerator: N(x)=n1xn2−n1−n2xn1+n2. Denominator: D(x)=xn1+n2−xn1−xn2+1.
First derivative of N(x): N′(x)=n1n2xn2−1−n2n1xn1−1. N′(1)=n1n2−n2n1=0. First derivative of D(x): D′(x)=(n1+n2)xn1+n2−1−n1xn1−1−n2xn2−1. D′(1)=(n1+n2)−n1−n2=0.
Since the first derivatives are also zero at x=1, we apply L'Hopital's Rule again. Second derivative of N(x): N′′(x)=n1n2(n2−1)xn2−2−n2n1(n1−1)xn1−2. N′′(1)=n1n2(n2−1)−n2n1(n1−1)=n1n2[(n2−1)−(n1−1)]=n1n2(n2−n1).
Second derivative of D(x): D′′(x)=(n1+n2)(n1+n2−1)xn1+n2−2−n1(n1−1)xn1−2−n2(n2−1)xn2−2. D′′(1)=(n1+n2)(n1+n2−1)−n1(n1−1)−n2(n2−1).
Now, substitute n1=2024 and n2=2022: N′′(1)=2024⋅2022(2022−2024)=2024⋅2022⋅(−2).
D′′(1)=(2024+2022)(2024+2022−1)−2024(2024−1)−2022(2022−1) D′′(1)=(4046)(4045)−2024(2023)−2022(2021) D′′(1)=(2024+2022)(2024+2021)−2024(2023)−2022(2021) D′′(1)=(20242+2024⋅2021+2022⋅2024+2022⋅2021)−2024⋅2023−2022⋅2021 D′′(1)=20242+2024⋅2021+2022⋅2024−2024⋅2023 D′′(1)=2024(2024+2021−2023)+2022⋅2024 D′′(1)=2024(4045−2023)+2022⋅2024 D′′(1)=2024(2022)+2022⋅2024=2⋅2024⋅2022.
By L'Hopital's Rule, the limit is: L=D′′(1)N′′(1)=2⋅2024⋅20222024⋅2022⋅(−2)=−1
