Question
Question: If $\int \frac{2e^x + 3e^{-x}}{3e^x + 4e^{-x}} dx = Ax + Blog(3e^{2x} + 4) + C$, then values of A an...
If ∫3ex+4e−x2ex+3e−xdx=Ax+Blog(3e2x+4)+C, then values of A and B are respectively (where C is a constant of integration.)
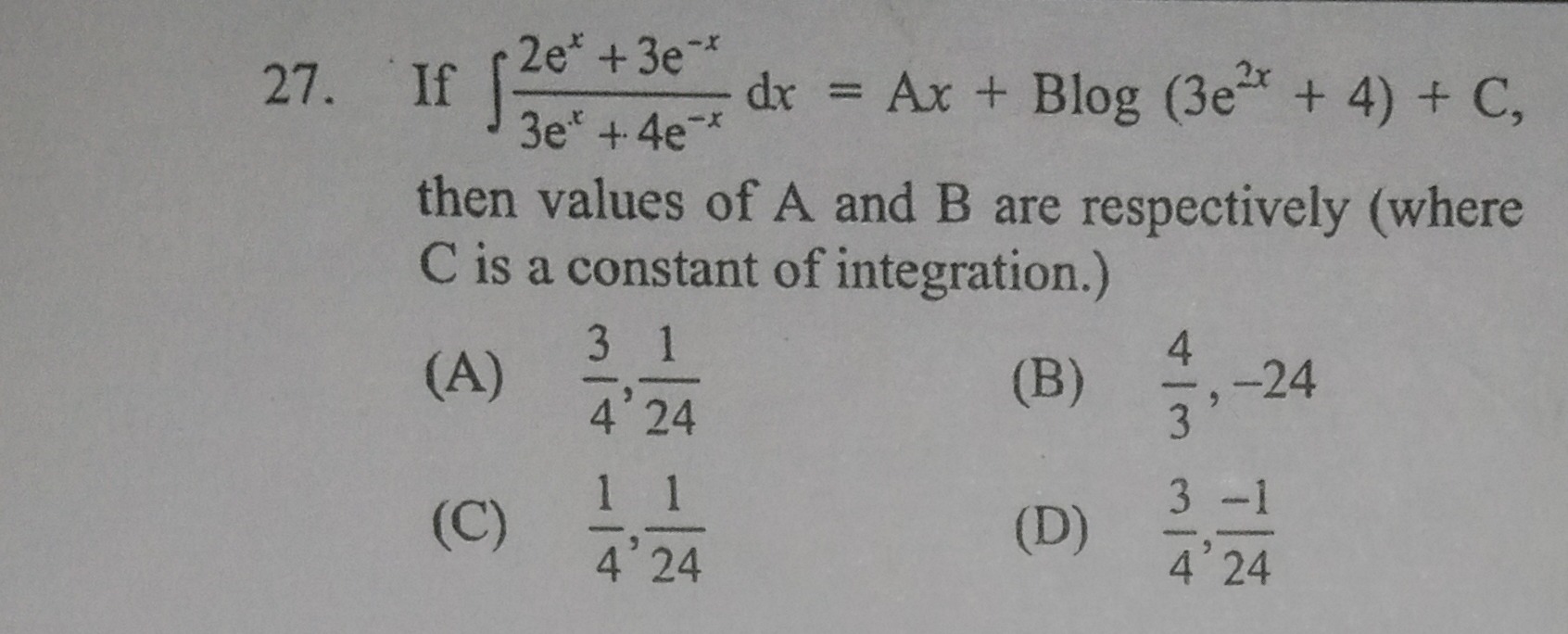
43,241
34,−24
41,241
43,24−1
(D)
Solution
Let the given integral be I.
I=∫3ex+4e−x2ex+3e−xdx
We are given that the result of the integral is Ax+Blog(3e2x+4)+C.
Let F(x)=Ax+Blog(3e2x+4)+C.
Then, the derivative of F(x) with respect to x must be equal to the integrand.
F′(x)=dxd(Ax+Blog(3e2x+4)+C)
F′(x)=A+Bdxd(log(3e2x+4))+0
Using the chain rule, dxd(log(u))=u1dxdu. Let u=3e2x+4.
dxdu=dxd(3e2x+4)=3dxd(e2x)+dxd(4)=3(e2x⋅2)+0=6e2x.
So, dxd(log(3e2x+4))=3e2x+46e2x.
Thus, F′(x)=A+B3e2x+46e2x.
We need to equate this to the integrand:
3ex+4e−x2ex+3e−x=A+B3e2x+46e2x
Let's simplify the integrand by multiplying the numerator and the denominator by ex:
(3ex+4e−x)ex(2ex+3e−x)ex=3e2x+4e02e2x+3e0=3e2x+42e2x+3.
Now, equate the simplified integrand to F′(x):
3e2x+42e2x+3=A+B3e2x+46e2x
Combine the terms on the right side by finding a common denominator:
A+B3e2x+46e2x=3e2x+4A(3e2x+4)+3e2x+46Be2x=3e2x+43Ae2x+4A+6Be2x
=3e2x+4(3A+6B)e2x+4A.
Equating the numerators:
2e2x+3=(3A+6B)e2x+4A.
This equation must hold for all values of x. By comparing the coefficients of e2x and the constant terms on both sides, we get a system of linear equations for A and B:
Comparing coefficients of e2x: 2=3A+6B
Comparing constant terms: 3=4A
From the second equation, 4A=3⟹A=43.
Substitute the value of A into the first equation:
2=3(43)+6B
2=49+6B
6B=2−49
6B=48−49
6B=−41
B=−4×61
B=−241.
Thus, the values of A and B are 43 and −241 respectively.
