Question
Question: If $f(x)$ is a polynomial of least degree, such that $\lim_{x\to0}\left(1+\frac{f(x)+x^2}{x^2}\right...
If f(x) is a polynomial of least degree, such that limx→0(1+x2f(x)+x2)1/x=e2, then f(2) is -
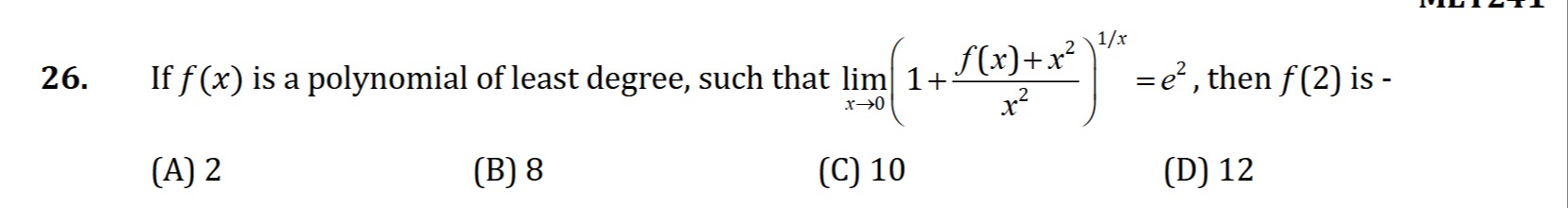
2
8
10
12
12
Solution
The given limit is limx→0(1+x2f(x)+x2)1/x=e2. This limit is of the form 1∞. We use the property limx→a(1+g(x))h(x)=elimx→ag(x)h(x). Here, g(x)=x2f(x)+x2 and h(x)=x1. For the limit to be finite, limx→0g(x)=limx→0x2f(x)+x2=0. This implies that f(x) must have terms that cancel out the x2 in the denominator and result in terms of degree higher than 2. Thus, f(x) must be of the form f(x)=−x2+a3x3+a4x4+…. Now, consider the exponent: limx→0g(x)h(x)=limx→0(x2f(x)+x2)(x1) Substitute f(x)=−x2+a3x3+a4x4+…: limx→0(x2−x2+a3x3+a4x4+⋯+x2)(x1) =limx→0(x2a3x3+a4x4+…)(x1) =limx→0(a3x+a4x2+…)(x1) =limx→0(a3+a4x+…) This limit equals a3. We are given that the original limit is e2, so the exponent must be 2: a3=2. Since f(x) is a polynomial of the least degree, we set all higher-order coefficients to zero. Thus, f(x)=−x2+2x3. We need to find f(2): f(2)=−(2)2+2(2)3=−4+2(8)=−4+16=12.
