Question
Question: If angle between $\overrightarrow{a}$ and $\overrightarrow{b}$ is $\pi/3$ then angle between $\overr...
If angle between a and b is π/3 then angle between a and −2b is :
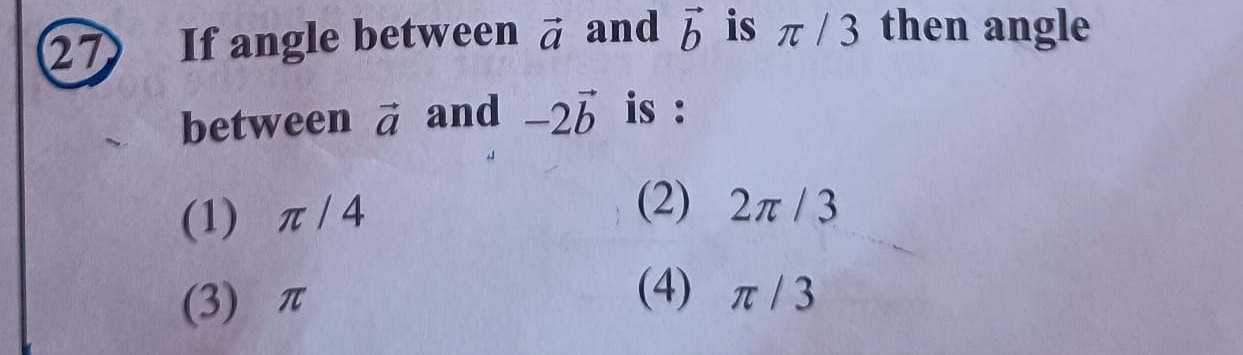
π/4
2π/3
π
π/3
2π/3
Solution
Let θ be the angle between vectors a and b. We are given θ=π/3. Let ϕ be the angle between vectors a and −2b. We want to find ϕ.
The angle between two vectors u and v can be found using the dot product formula: cosθ=∣u∣∣v∣u⋅v
For the angle between a and b, we have: cos(π/3)=∣a∣∣b∣a⋅b
Since cos(π/3)=1/2, we have ∣a∣∣b∣a⋅b=1/2.
For the angle ϕ between a and −2b, we have: cosϕ=∣a∣∣−2b∣a⋅(−2b)
Using the properties of the dot product and vector magnitude: a⋅(−2b)=−2(a⋅b) ∣−2b∣=∣−2∣∣b∣=2∣b∣
Substitute these into the formula for cosϕ: cosϕ=∣a∣(2∣b∣)−2(a⋅b) cosϕ=∣a∣∣b∣−(a⋅b)
We know that ∣a∣∣b∣a⋅b=cos(π/3)=1/2. So, cosϕ=−(1/2)=−1/2.
The angle ϕ between two vectors is conventionally taken to be in the range [0,π]. We need to find ϕ∈[0,π] such that cosϕ=−1/2. The angle is ϕ=2π/3.
