Solveeit Logo
Login

Question

Question: If a = i + 5k, b = 2i + 3k, c = 4i - j + 2k and d=i-j then (c-a) (bxd) =...

If a = i + 5k, b = 2i + 3k, c = 4i - j + 2k and d=i-j then (c-a) (bxd) =

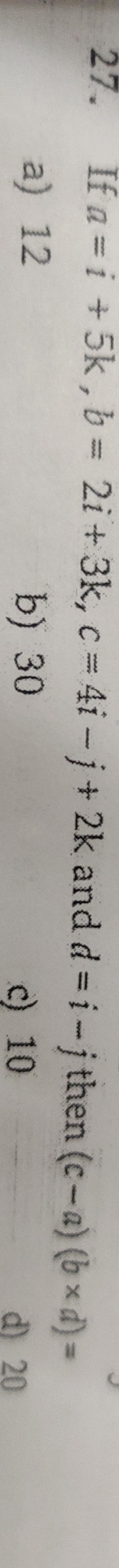
A

12

B

30

C

10

D

20

Answer

12

Explanation

Solution

To find the value of (c-a) . (b x d), follow these steps:

  1. Express the vectors in component form:

    • a=⟨1,0,5⟩a = \langle 1, 0, 5 \rangle
    • b=⟨2,0,3⟩b = \langle 2, 0, 3 \rangle
    • c=⟨4,−1,2⟩c = \langle 4, -1, 2 \rangle
    • d=⟨1,−1,0⟩d = \langle 1, -1, 0 \rangle

  2. Calculate c−ac - a:

    c−a=⟨4−1,−1−0,2−5⟩=⟨3,−1,−3⟩c - a = \langle 4 - 1, -1 - 0, 2 - 5 \rangle = \langle 3, -1, -3 \rangle

  3. Compute the cross product b×db \times d:

    b×d=∣ijk2031−10∣=i(0−(−3))−j(0−3)+k(−2−0)=3i+3j−2k=⟨3,3,−2⟩b \times d = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 2 & 0 & 3 \\ 1 & -1 & 0 \end{vmatrix} = \mathbf{i}(0 - (-3)) - \mathbf{j}(0 - 3) + \mathbf{k}(-2 - 0) = 3\mathbf{i} + 3\mathbf{j} - 2\mathbf{k} = \langle 3, 3, -2 \rangle

  4. Compute the dot product (c−a)⋅(b×d)(c - a) \cdot (b \times d):

    (c−a)⋅(b×d)=⟨3,−1,−3⟩⋅⟨3,3,−2⟩=(3×3)+(−1×3)+(−3×−2)=9−3+6=12(c - a) \cdot (b \times d) = \langle 3, -1, -3 \rangle \cdot \langle 3, 3, -2 \rangle = (3 \times 3) + (-1 \times 3) + (-3 \times -2) = 9 - 3 + 6 = 12

Therefore, (c−a)⋅(b×d)=12(c - a) \cdot (b \times d) = 12.