Question
Question: $\frac{1+x}{x \sin^2 (x+\log x)}$...
xsin2(x+logx)1+x
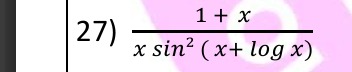
Answer
−cot(x+logx)+C
Explanation
Solution
To evaluate the integral ∫xsin2(x+logx)1+xdx, we can use the method of substitution.
Let t=x+logx.
Now, we find the differential dt by differentiating t with respect to x: dt=dxd(x+logx)dx dt=(1+x1)dx dt=(xx+1)dx
Observe that the term x1+xdx is present in the integrand. So, the integral can be rewritten as: ∫sin2(x+logx)1⋅(x1+x)dx
Substitute t=x+logx and dt=x1+xdx into the integral: ∫sin2t1dt
We know that sin2t1=csc2t. So, the integral becomes: ∫csc2tdt
The standard integral of csc2t is −cott+C, where C is the constant of integration. Thus, ∫csc2tdt=−cott+C
Finally, substitute back t=x+logx: −cot(x+logx)+C
