Solveeit Logo
Login

Question

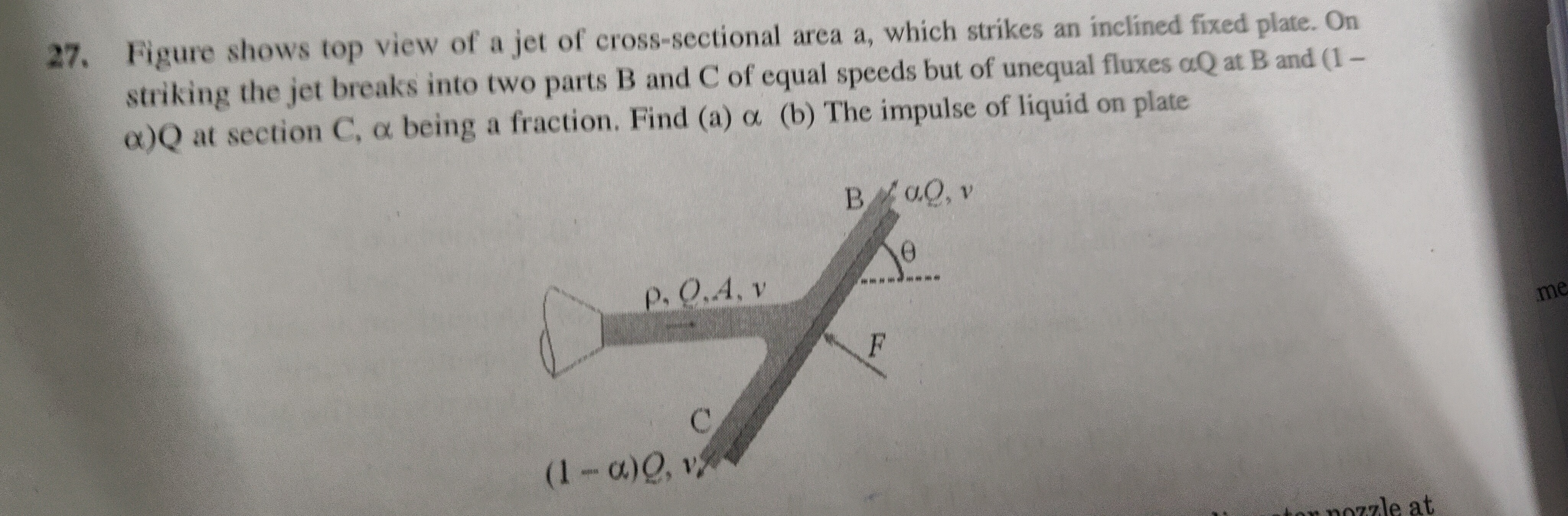
Question: Figure shows top view of a jet of cross-sectional area a, which strikes an inclined fixed plate. On ...

Figure shows top view of a jet of cross-sectional area a, which strikes an inclined fixed plate. On striking the jet breaks into two parts B and C of equal speeds but of unequal fluxes α\alphaQ at B and (1-α\alpha)Q at section C, α\alpha being a fraction. Find (a) α\alpha (b) The impulse of liquid on plate

A

a) α=11−sin⁡θ\alpha = \frac{1}{1 - \sin \theta}, b) Impulse =ρQv(1−sin⁡θ+cos⁡θ1−sin⁡θ)= \rho Q v \left(\frac{1 - \sin \theta + \cos \theta}{1 - \sin \theta}\right)

B

a) α=11+sin⁡θ\alpha = \frac{1}{1 + \sin \theta}, b) Impulse =ρQv(1+sin⁡θ+cos⁡θ1+sin⁡θ)= \rho Q v \left(\frac{1 + \sin \theta + \cos \theta}{1 + \sin \theta}\right)

C

a) α=11−sin⁡θ\alpha = \frac{1}{1 - \sin \theta}, b) Impulse =ρQv(1+sin⁡θ+cos⁡θ1−sin⁡θ)= \rho Q v \left(\frac{1 + \sin \theta + \cos \theta}{1 - \sin \theta}\right)

D

a) α=11+sin⁡θ\alpha = \frac{1}{1 + \sin \theta}, b) Impulse =ρQv(1−sin⁡θ+cos⁡θ1+sin⁡θ)= \rho Q v \left(\frac{1 - \sin \theta + \cos \theta}{1 + \sin \theta}\right)

Answer

a) α=11−sin⁡θ\alpha = \frac{1}{1 - \sin \theta}, b) Impulse =ρQv(1−sin⁡θ+cos⁡θ1−sin⁡θ)= \rho Q v \left(\frac{1 - \sin \theta + \cos \theta}{1 - \sin \theta}\right)

Explanation

Solution

Let the initial velocity of the jet be v⃗i\vec{v}_i with speed vv. We assume the initial jet is perpendicular to the plate, so the angle of incidence with the normal to the plate is 0∘0^\circ. Stream B leaves at an angle θ\theta with the normal, so its angle of reflection is θ\theta. Stream C flows along the plate.

We resolve velocities into components perpendicular and parallel to the plate. Initial velocity: v⊥i=vv_{\perp i} = v (normal), v∥i=0v_{\parallel i} = 0 (parallel). For stream B: v⊥B=−vcos⁡θv_{\perp B} = -v \cos \theta (normal), v∥B=vsin⁡θv_{\parallel B} = v \sin \theta (parallel). For stream C: v⊥C=0v_{\perp C} = 0 (normal), v∥C=vv_{\parallel C} = v (parallel).

(a) Finding α\alpha: Conservation of momentum parallel to the plate: Initial momentum flux parallel to the plate: ρQv∥i=0\rho Q v_{\parallel i} = 0. Final momentum flux parallel to the plate: ρ(αQ)v∥B+ρ((1−α)Q)v∥C=ρ(αQ)(vsin⁡θ)+ρ((1−α)Q)v\rho (\alpha Q) v_{\parallel B} + \rho ((1-\alpha) Q) v_{\parallel C} = \rho (\alpha Q) (v \sin \theta) + \rho ((1-\alpha) Q) v. By conservation of momentum: 0=ραQvsin⁡θ+ρ(1−α)Qv0 = \rho \alpha Q v \sin \theta + \rho (1-\alpha) Q v. Dividing by ρQv\rho Q v: 0=αsin⁡θ+(1−α)  ⟹  α(1−sin⁡θ)=1  ⟹  α=11−sin⁡θ0 = \alpha \sin \theta + (1-\alpha) \implies \alpha (1 - \sin \theta) = 1 \implies \alpha = \frac{1}{1 - \sin \theta}.

(b) Impulse of liquid on the plate: The impulse is the change in momentum. We consider the momentum change in the direction perpendicular to the plate. Initial momentum flux perpendicular to the plate: P⊥i=ρQv⊥i=ρQvP_{\perp i} = \rho Q v_{\perp i} = \rho Q v. Final momentum flux perpendicular to the plate: P⊥f=ρ(αQ)v⊥B+ρ((1−α)Q)v⊥C=ρ(αQ)(−vcos⁡θ)+0=−ραQvcos⁡θP_{\perp f} = \rho (\alpha Q) v_{\perp B} + \rho ((1-\alpha) Q) v_{\perp C} = \rho (\alpha Q) (-v \cos \theta) + 0 = -\rho \alpha Q v \cos \theta. The impulse in the perpendicular direction is ΔP⊥=P⊥f−P⊥i=−ραQvcos⁡θ−ρQv=−ρQv(1+αcos⁡θ)\Delta P_{\perp} = P_{\perp f} - P_{\perp i} = -\rho \alpha Q v \cos \theta - \rho Q v = -\rho Q v (1 + \alpha \cos \theta). Substituting α=11−sin⁡θ\alpha = \frac{1}{1 - \sin \theta}: ΔP⊥=−ρQv(1+cos⁡θ1−sin⁡θ)=−ρQv(1−sin⁡θ+cos⁡θ1−sin⁡θ)\Delta P_{\perp} = -\rho Q v \left(1 + \frac{\cos \theta}{1 - \sin \theta}\right) = -\rho Q v \left(\frac{1 - \sin \theta + \cos \theta}{1 - \sin \theta}\right). The impulse on the plate is equal and opposite to the impulse on the liquid. Impulse on the plate I=−ΔP⊥=ρQv(1−sin⁡θ+cos⁡θ1−sin⁡θ)I = -\Delta P_{\perp} = \rho Q v \left(\frac{1 - \sin \theta + \cos \theta}{1 - \sin \theta}\right). The impulse in the direction parallel to the plate is zero.