Question

Which of the following is/are conservative force(s)?

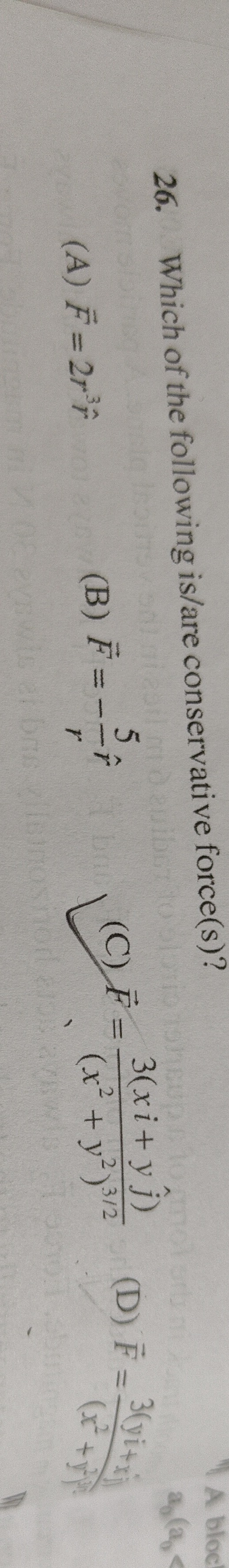
• A. $\overrightarrow{F} = 2\overrightarrow{r}$
• B. $\overrightarrow{F}=-\frac{5}{r}\hat{r}$
• C. $\overrightarrow{F} = \frac{3(x\hat{i}+y\hat{j})}{(x^2 + y^2)^{3/2}}$
• D. $\overrightarrow{F} = \frac{3(y\hat{i}+x\hat{j}}{(x^{2}+}$

Answer 1

Answer: (A), (B), (C)

A, B, C

Answer 2

A force $\overrightarrow{F}$ is conservative if its curl is zero ($\nabla \times \overrightarrow{F} = \overrightarrow{0}$) or if it can be expressed as the negative gradient of a scalar potential function ($\overrightarrow{F} = -\nabla U$). All central forces (forces directed along the position vector $\overrightarrow{r}$ and whose magnitude depends only on $r$) are conservative.

1. Option A ($\overrightarrow{F} = 2\overrightarrow{r}$): This is a central force of the form $f(r)\hat{r}$ where $f(r) = 2r$. Its curl is calculated to be zero. Hence, it is conservative.
2. Option B ($\overrightarrow{F}=-\frac{5}{r}\hat{r}$): This is a central force of the form $f(r)\hat{r}$ where $f(r) = -5/r$. All central forces are conservative.
3. Option C ($\overrightarrow{F} = \frac{3(x\hat{i}+y\hat{j})}{(x^2 + y^2)^{3/2}}$): This can be rewritten as $\overrightarrow{F} = \frac{3\overrightarrow{r}}{r^3} = \frac{3}{r^2}\hat{r}$ in 2D. This is a central force, and its curl is calculated to be zero. Hence, it is conservative.
4. Option D ($\overrightarrow{F} = \frac{3(y\hat{i}+x\hat{j}}{(x^{2}+}$): Assuming a reasonable completion for the denominator (e.g., $(x^2+y^2)^{3/2}$), the curl of this force is calculated and found to be non-zero. Therefore, it is not a conservative force.