Question

The unit vector perpendicular to the plane 4x - 3y + 12z = 15 is

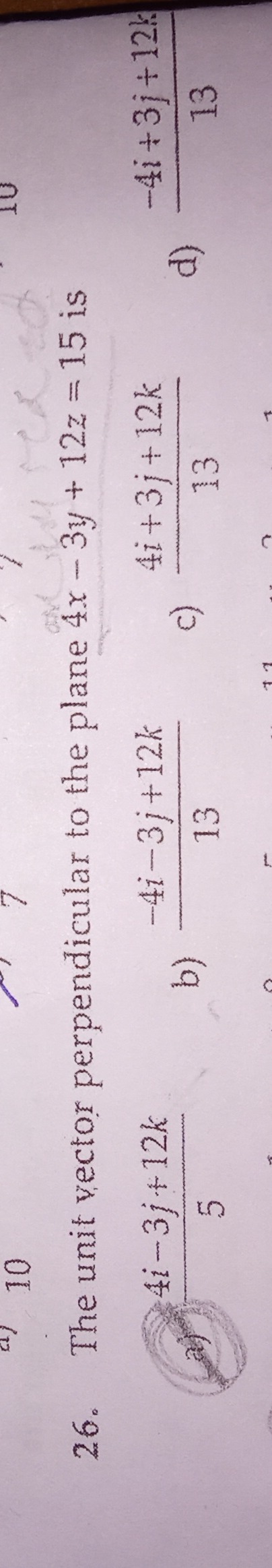
• A. $\frac{4i-3j+12k}{5}$
• B. $\frac{-4i-3j+12k}{13}$
• C. $\frac{4i+3j+12k}{13}$
• D. $\frac{-4i+3j+12k}{13}$

Answer 1

None of the given options.

Answer 2

For a plane given by

$4x-3y+12z=15$,

the normal vector is

$\mathbf{n}=(4,-3,12)$.

Its magnitude is

$|\mathbf{n}|=\sqrt{4^2+(-3)^2+12^2}=\sqrt{16+9+144}=\sqrt{169}=13$.

Thus, the unit vector perpendicular to the plane is

$\frac{\mathbf{n}}{|\mathbf{n}|}=\frac{4i-3j+12k}{13}$.

None of the given options match $\frac{4i-3j+12k}{13}$.