Question

The potential energy function for the force between two atoms in a diatomic molecule is

$U(x) = \frac{a}{x^{12}} - \frac{b}{x^{6}}$

Where a and b are positive constants and x is the distance between the atoms. How much energy must be supplied to separate the two atoms.

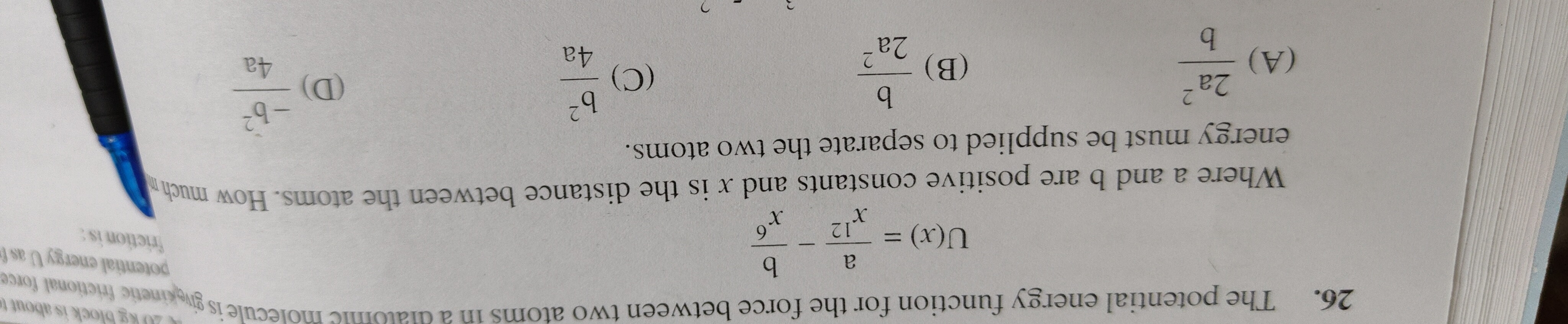
• A. $\frac{b}{2a^{2}}$
• B. $\frac{2a^{2}}{b}$
• C. $\frac{4a}{b^{2}}$
• D. $-\frac{4a}{b^{2}}$

Answer 1

None of the given options are correct. The correct answer is $\frac{b^2}{4a}$.

Answer 2

The dissociation energy is the difference between the potential energy at infinite separation and the minimum potential energy at equilibrium.

1. $U(x=\infty) = 0$.

2. Find equilibrium distance $x_0$ by setting $\frac{dU}{dx} = 0$. $U(x) = ax^{-12} - bx^{-6}$ $\frac{dU}{dx} = -12ax^{-13} + 6bx^{-7} = 0$ $x_0^6 = \frac{2a}{b}$

3. Calculate $U_{equilibrium}$ by substituting $x_0^6$ into $U(x)$. $U_{equilibrium} = \frac{a}{(x_0^6)^2} - \frac{b}{x_0^6} = \frac{a}{(2a/b)^2} - \frac{b}{(2a/b)} = \frac{b^2}{4a} - \frac{b^2}{2a} = -\frac{b^2}{4a}$.

4. Energy supplied = $U(x=\infty) - U_{equilibrium} = 0 - (-\frac{b^2}{4a}) = \frac{b^2}{4a}$.