Question

The equation of the parabola whose equation of directrix is 3x +4y-1 = 0 and focus is at (-1,3) is ax²+bxy+cy²+56x-142y+249 = 0. Then the value of a+b+c is

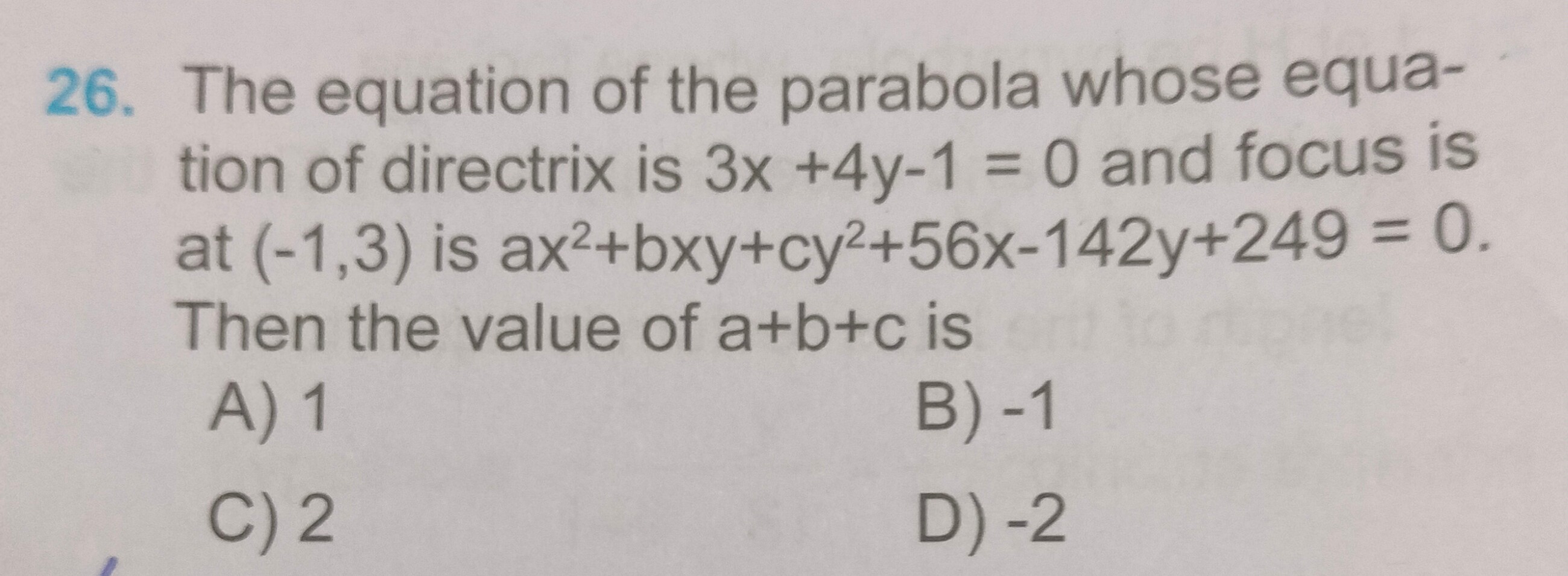
• A. 1
• B. -1
• C. 2
• D. -2

Answer 1

Answer: (A)

1

Answer 2

The fundamental definition of a parabola states that it is the locus of a point that is equidistant from a fixed point (the focus) and a fixed line (the directrix).

Given:

• Focus S = (-1, 3)
• Equation of the directrix L: $3x + 4y - 1 = 0$

Let P(x, y) be any point on the parabola.

1. Distance from P to the focus (PS):
   Using the distance formula, $PS = \sqrt{(x - (-1))^2 + (y - 3)^2}$
   $PS = \sqrt{(x + 1)^2 + (y - 3)^2}$

2. Distance from P to the directrix (PM):
   The perpendicular distance from a point $(x_0, y_0)$ to a line $Ax + By + C = 0$ is given by the formula $PM = \frac{|Ax_0 + By_0 + C|}{\sqrt{A^2 + B^2}}$.
   Here, $(x_0, y_0) = (x, y)$, $A = 3$, $B = 4$, $C = -1$.
   $PM = \frac{|3x + 4y - 1|}{\sqrt{3^2 + 4^2}}$
   $PM = \frac{|3x + 4y - 1|}{\sqrt{9 + 16}}$
   $PM = \frac{|3x + 4y - 1|}{\sqrt{25}}$
   $PM = \frac{|3x + 4y - 1|}{5}$

3. Equate PS and PM (PS = PM):
   $\sqrt{(x + 1)^2 + (y - 3)^2} = \frac{|3x + 4y - 1|}{5}$

4. Square both sides to eliminate the square root and absolute value:
   $(x + 1)^2 + (y - 3)^2 = \left(\frac{3x + 4y - 1}{5}\right)^2$
   $(x^2 + 2x + 1) + (y^2 - 6y + 9) = \frac{(3x + 4y - 1)^2}{25}$
   $x^2 + y^2 + 2x - 6y + 10 = \frac{(3x)^2 + (4y)^2 + (-1)^2 + 2(3x)(4y) + 2(4y)(-1) + 2(3x)(-1)}{25}$
   $x^2 + y^2 + 2x - 6y + 10 = \frac{9x^2 + 16y^2 + 1 + 24xy - 8y - 6x}{25}$

5. Multiply both sides by 25 and rearrange the terms:
   $25(x^2 + y^2 + 2x - 6y + 10) = 9x^2 + 16y^2 + 24xy - 6x - 8y + 1$
   $25x^2 + 25y^2 + 50x - 150y + 250 = 9x^2 + 16y^2 + 24xy - 6x - 8y + 1$
   Move all terms to one side to match the given general form $ax^2+bxy+cy^2+56x-142y+249 = 0$:
   $(25x^2 - 9x^2) + (25y^2 - 16y^2) - 24xy + (50x - (-6x)) + (-150y - (-8y)) + (250 - 1) = 0$
   $16x^2 + 9y^2 - 24xy + (50x + 6x) + (-150y + 8y) + 249 = 0$
   $16x^2 - 24xy + 9y^2 + 56x - 142y + 249 = 0$

6. Compare with the given equation $ax^2+bxy+cy^2+56x-142y+249 = 0$:
   By comparing the coefficients, we get:
   $a = 16$
   $b = -24$
   $c = 9$

7. Calculate a + b + c:
   $a + b + c = 16 + (-24) + 9$
   $a + b + c = 16 - 24 + 9$
   $a + b + c = -8 + 9$
   $a + b + c = 1$