Solveeit Logo
Login

Question

Question: $\lim_{x \to 1} \left( \frac{1}{x^{2024}-1} - \frac{1}{x^{2022}-1} \right)$...

lim⁡x→1(1x2024−1−1x2022−1)\lim_{x \to 1} \left( \frac{1}{x^{2024}-1} - \frac{1}{x^{2022}-1} \right)

Answer

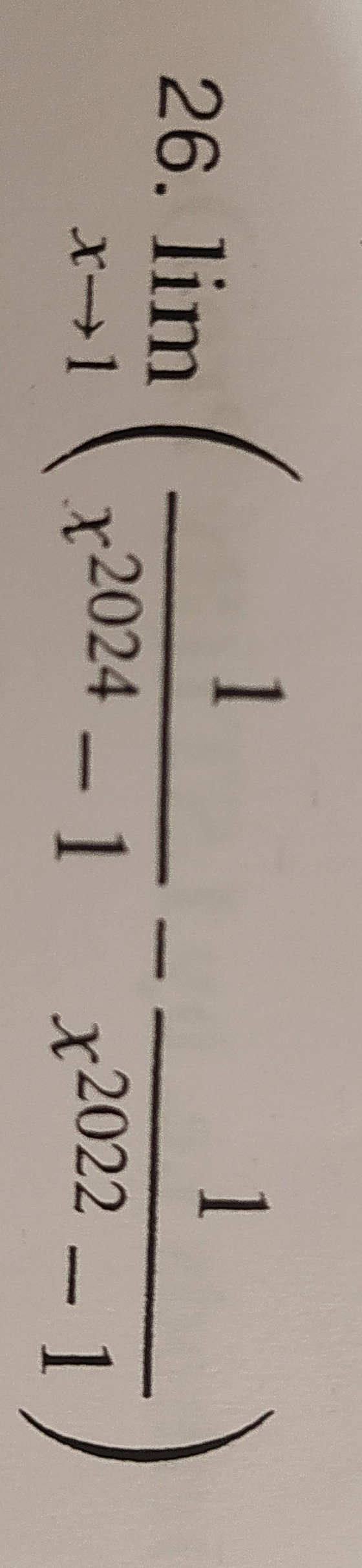
The limit does not exist.

Explanation

Solution

Let the given limit be LL.

L=lim⁡x→1(1x2024−1−1x2022−1)L = \lim_{x \to 1} \left( \frac{1}{x^{2024}-1} - \frac{1}{x^{2022}-1} \right)

Combine the fractions:

L=lim⁡x→1(x2022−1)−(x2024−1)(x2024−1)(x2022−1)L = \lim_{x \to 1} \frac{(x^{2022}-1) - (x^{2024}-1)}{(x^{2024}-1)(x^{2022}-1)}

L=lim⁡x→1x2022−1−x2024+1(x2024−1)(x2022−1)L = \lim_{x \to 1} \frac{x^{2022} - 1 - x^{2024} + 1}{(x^{2024}-1)(x^{2022}-1)}

L=lim⁡x→1x2022−x2024(x2024−1)(x2022−1)L = \lim_{x \to 1} \frac{x^{2022} - x^{2024}}{(x^{2024}-1)(x^{2022}-1)}

Factor out x2022x^{2022} from the numerator:

L=lim⁡x→1x2022(1−x2)(x2024−1)(x2022−1)L = \lim_{x \to 1} \frac{x^{2022}(1 - x^2)}{(x^{2024}-1)(x^{2022}-1)}

Factor 1−x2=(1−x)(1+x)=−(x−1)(x+1)1-x^2 = (1-x)(1+x) = -(x-1)(x+1):

L=lim⁡x→1−x2022(x−1)(x+1)(x2024−1)(x2022−1)L = \lim_{x \to 1} \frac{-x^{2022}(x-1)(x+1)}{(x^{2024}-1)(x^{2022}-1)}

We use the factorization an−bn=(a−b)(an−1+an−2b+⋯+abn−2+bn−1)a^n - b^n = (a-b)(a^{n-1} + a^{n-2}b + \dots + ab^{n-2} + b^{n-1}).

Let a=xa=x and b=1b=1. Then xn−1=(x−1)(xn−1+xn−2+⋯+x+1)x^n - 1 = (x-1)(x^{n-1} + x^{n-2} + \dots + x + 1).

Let Pn(x)=xn−1+xn−2+⋯+x+1P_n(x) = x^{n-1} + x^{n-2} + \dots + x + 1. Note that lim⁡x→1Pn(x)=n\lim_{x \to 1} P_n(x) = n.

So, x2024−1=(x−1)P2024(x)x^{2024}-1 = (x-1)P_{2024}(x) and x2022−1=(x−1)P2022(x)x^{2022}-1 = (x-1)P_{2022}(x).

Substitute these into the expression for LL:

L=lim⁡x→1−x2022(x−1)(x+1)((x−1)P2024(x))((x−1)P2022(x))L = \lim_{x \to 1} \frac{-x^{2022}(x-1)(x+1)}{((x-1)P_{2024}(x))((x-1)P_{2022}(x))}

L=lim⁡x→1−x2022(x−1)(x+1)(x−1)2P2024(x)P2022(x)L = \lim_{x \to 1} \frac{-x^{2022}(x-1)(x+1)}{(x-1)^2 P_{2024}(x) P_{2022}(x)}

Cancel one factor of (x−1)(x-1) from the numerator and denominator:

L=lim⁡x→1−x2022(x+1)(x−1)P2024(x)P2022(x)L = \lim_{x \to 1} \frac{-x^{2022}(x+1)}{(x-1) P_{2024}(x) P_{2022}(x)}

Let's rewrite the expression slightly:

L=lim⁡x→1−x2022(x+1)P2024(x)P2022(x)⋅1x−1L = \lim_{x \to 1} \frac{-x^{2022}(x+1)}{P_{2024}(x) P_{2022}(x)} \cdot \frac{1}{x-1}

As x→1x \to 1, the first part of the expression approaches:

lim⁡x→1−x2022(x+1)P2024(x)P2022(x)=−(1)2022(1+1)P2024(1)P2022(1)=−1(2)2024⋅2022=−22024⋅2022\lim_{x \to 1} \frac{-x^{2022}(x+1)}{P_{2024}(x) P_{2022}(x)} = \frac{-(1)^{2022}(1+1)}{P_{2024}(1) P_{2022}(1)} = \frac{-1(2)}{2024 \cdot 2022} = \frac{-2}{2024 \cdot 2022}

So the limit becomes:

L=(−22024⋅2022)⋅lim⁡x→11x−1L = \left( \frac{-2}{2024 \cdot 2022} \right) \cdot \lim_{x \to 1} \frac{1}{x-1}

The limit lim⁡x→11x−1\lim_{x \to 1} \frac{1}{x-1} does not exist. As x→1+x \to 1^+, 1x−1→+∞\frac{1}{x-1} \to +\infty. As x→1−x \to 1^-, 1x−1→−∞\frac{1}{x-1} \to -\infty.

Since the first factor −22024⋅2022\frac{-2}{2024 \cdot 2022} is a non-zero finite number, the overall limit does not exist.