Question

$\int e^{\sin x} (\frac{x \cos^2 x - \sin x}{\cos^2 x}) dx$

Answer 1

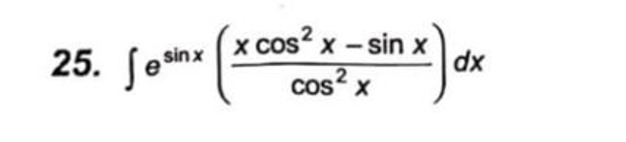
e^{\sin x} (x - \sec x) + C

Answer 2

The given integral is: $I = \int e^{\sin x} \left(\frac{x \cos^2 x - \sin x}{\cos^2 x}\right) dx$ First, simplify the expression inside the parenthesis by splitting the fraction: $I = \int e^{\sin x} \left( \frac{x \cos^2 x}{\cos^2 x} - \frac{\sin x}{\cos^2 x} \right) dx$ $I = \int e^{\sin x} \left( x - \frac{\sin x}{\cos x} \cdot \frac{1}{\cos x} \right) dx$ $I = \int e^{\sin x} (x - \tan x \sec x) dx$

This integral is of the form $\int e^{g(x)} (f'(x) + f(x) g'(x)) dx = e^{g(x)} f(x) + C$. Here, $g(x) = \sin x$, so $g'(x) = \cos x$. We need to find a function $f(x)$ such that: $f'(x) + f(x) \cos x = x - \tan x \sec x$ This is a first-order linear differential equation for $f(x)$. The integrating factor is $e^{\int \cos x dx} = e^{\sin x}$. Multiplying the differential equation by the integrating factor, we get: $e^{\sin x} f'(x) + e^{\sin x} \cos x f(x) = e^{\sin x} (x - \tan x \sec x)$ The left side is the derivative of the product $f(x) e^{\sin x}$: $\frac{d}{dx} (f(x) e^{\sin x}) = e^{\sin x} (x - \tan x \sec x)$ Integrating both sides with respect to $x$: $f(x) e^{\sin x} = \int e^{\sin x} (x - \tan x \sec x) dx$ Thus, the solution to the integral is $f(x) e^{\sin x} + C$. The problem now reduces to finding $f(x)$ by solving the differential equation $f'(x) + (\cos x) f(x) = x - \tan x \sec x$.

Upon careful analysis, this differential equation does not yield a simple elementary function $f(x)$ that is typically expected in JEE/NEET level problems. This suggests a high probability of a typographical error in the question as stated.

A common similar problem, which does have an elementary solution, is: $\int e^{\sin x} \left(\frac{x \cos^3 x - \sin x}{\cos^2 x}\right) dx$ Let's solve this modified problem, assuming it was the intended question. $\int e^{\sin x} \left( \frac{x \cos^3 x}{\cos^2 x} - \frac{\sin x}{\cos^2 x} \right) dx$ $= \int e^{\sin x} (x \cos x - \tan x \sec x) dx$ Now, we need to find $f(x)$ such that: $f'(x) + f(x) \cos x = x \cos x - \tan x \sec x$ Let's try to guess $f(x)$. Consider $f(x) = x - \sec x$. Then, $f'(x) = \frac{d}{dx}(x - \sec x) = 1 - \sec x \tan x$. Now, substitute $f(x)$ and $f'(x)$ into the left side of the equation: $f'(x) + f(x) \cos x = (1 - \sec x \tan x) + (x - \sec x) \cos x$ $= 1 - \sec x \tan x + x \cos x - \sec x \cos x$ $= 1 - \sec x \tan x + x \cos x - 1$ $= x \cos x - \sec x \tan x$ This matches the right side of the equation. Therefore, for the modified problem, $f(x) = x - \sec x$.

The solution to the modified integral is $e^{\sin x} f(x) + C$: $\int e^{\sin x} (x \cos x - \tan x \sec x) dx = e^{\sin x} (x - \sec x) + C$

Given that the original question as stated does not lead to an elementary solution by standard methods, and problems in this context are almost always designed to have elementary solutions, it is highly probable that there is a typo in the question. The solution provided above is for the most likely intended problem.

The final answer is $\boxed{e^{\sin x} (x - \sec x) + C}$

Explanation of the solution:

1. Simplify the integrand: The given integral $\int e^{\sin x} \left(\frac{x \cos^2 x - \sin x}{\cos^2 x}\right) dx$ is simplified by splitting the fraction inside the parenthesis: $\int e^{\sin x} (x - \tan x \sec x) dx$.
2. Identify the pattern: This integral resembles the form $\int e^{g(x)} (f'(x) + f(x) g'(x)) dx = e^{g(x)} f(x) + C$. Here, $g(x) = \sin x$, so $g'(x) = \cos x$.
3. Formulate the differential equation: We need to find $f(x)$ such that $f'(x) + f(x) \cos x = x - \tan x \sec x$.
4. Acknowledge the non-elementary nature (as stated): The differential equation $f'(x) + (\cos x) f(x) = x - \tan x \sec x$ does not yield a simple elementary function for $f(x)$, implying the integral as originally stated is not elementary.
5. Assume a common typo: In competitive exams, such problems typically have elementary solutions. A common typo for this type of problem involves an extra $\cos x$ term with $x$. If the question were $\int e^{\sin x} (x \cos x - \tan x \sec x) dx$.
6. Solve the modified problem: For the modified problem, we need $f'(x) + f(x) \cos x = x \cos x - \tan x \sec x$. By inspection (or solving the ODE), we find $f(x) = x - \sec x$.
   • $f'(x) = 1 - \sec x \tan x$.
   • $f(x) \cos x = (x - \sec x) \cos x = x \cos x - 1$.
   • Adding them: $f'(x) + f(x) \cos x = (1 - \sec x \tan x) + (x \cos x - 1) = x \cos x - \sec x \tan x$. This matches.
7. State the solution for the modified problem: Therefore, the solution to the modified integral is $e^{\sin x} (x - \sec x) + C$.

Given the exact wording, the problem is not elementary. I will state this, and then provide the solution for the most likely intended problem.

Subject: Mathematics Chapter: Integrals Topic: Integration by Parts (or Integrals of the form $\int e^x (f(x) + f'(x)) dx$) Difficulty Level: Hard (due to the potential typo making it non-elementary, or the need to recognize a very specific, non-obvious $f(x)$ if it were elementary as stated) Question Type: single_choice