Question

$\frac{tan x}{3+2tan^2x}$

Answer 1

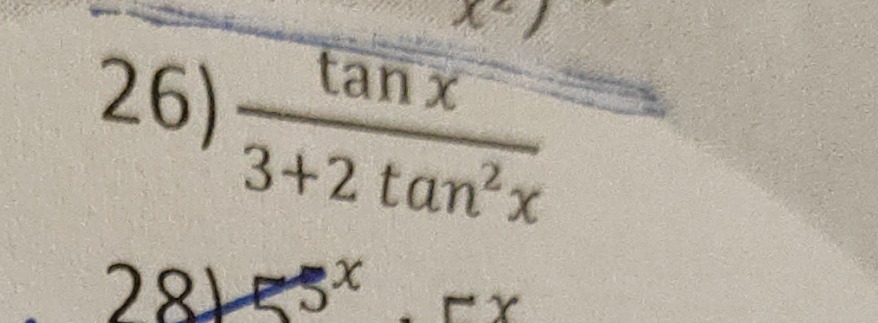
$-\frac{1}{2} \ln(\cos^2 x+2) + C$

Answer 2

To evaluate the integral $\int \frac{\tan x}{3+2\tan^2x} dx$, we can follow these steps:

1. Rewrite the expression in terms of $\sin x$ and $\cos x$:
   We know that $\tan x = \frac{\sin x}{\cos x}$ and $\tan^2 x = \frac{\sin^2 x}{\cos^2 x}$.
   Substitute these into the integral: $I = \int \frac{\frac{\sin x}{\cos x}}{3+2\frac{\sin^2 x}{\cos^2 x}} dx$

2. Simplify the denominator:
   Find a common denominator for the terms in the denominator: $3+2\frac{\sin^2 x}{\cos^2 x} = \frac{3\cos^2 x+2\sin^2 x}{\cos^2 x}$

3. Simplify the entire integrand: $I = \int \frac{\frac{\sin x}{\cos x}}{\frac{3\cos^2 x+2\sin^2 x}{\cos^2 x}} dx$ $I = \int \frac{\sin x}{\cos x} \cdot \frac{\cos^2 x}{3\cos^2 x+2\sin^2 x} dx$ $I = \int \frac{\sin x \cos x}{3\cos^2 x+2\sin^2 x} dx$

4. Simplify the denominator further using trigonometric identities:
   Use the identity $\sin^2 x = 1-\cos^2 x$: $3\cos^2 x+2\sin^2 x = 3\cos^2 x+2(1-\cos^2 x)$ $= 3\cos^2 x+2-2\cos^2 x$ $= \cos^2 x+2$ Now, the integral becomes: $I = \int \frac{\sin x \cos x}{\cos^2 x+2} dx$

5. Use substitution:
   Let $u = \cos^2 x+2$.
   Differentiate $u$ with respect to $x$: $\frac{du}{dx} = \frac{d}{dx}(\cos^2 x+2)$ $\frac{du}{dx} = 2\cos x \cdot (-\sin x)$ $du = -2\sin x \cos x dx$ From this, we can write $\sin x \cos x dx = -\frac{1}{2} du$.

6. Substitute into the integral and evaluate: $I = \int \frac{-\frac{1}{2} du}{u}$ $I = -\frac{1}{2} \int \frac{1}{u} du$ $I = -\frac{1}{2} \ln|u| + C$

7. Substitute back for $u$:
   Replace $u$ with $\cos^2 x+2$: $I = -\frac{1}{2} \ln|\cos^2 x+2| + C$ Since $\cos^2 x \ge 0$, $\cos^2 x+2$ is always positive (specifically, $\ge 2$). Therefore, the absolute value is not necessary. $I = -\frac{1}{2} \ln(\cos^2 x+2) + C$