Solveeit Logo
Login

Question

Question: Assuming potential energy 'U' at ground level to be zero. All objects are made up of same material....

Assuming potential energy 'U' at ground level to be zero.

All objects are made up of same material. UPU_P = Potential energy of solid sphere UQU_Q = Potential energy of solid cube URU_R = Potential energy of solid cone USU_S = Potential energy of solid cylinder

A

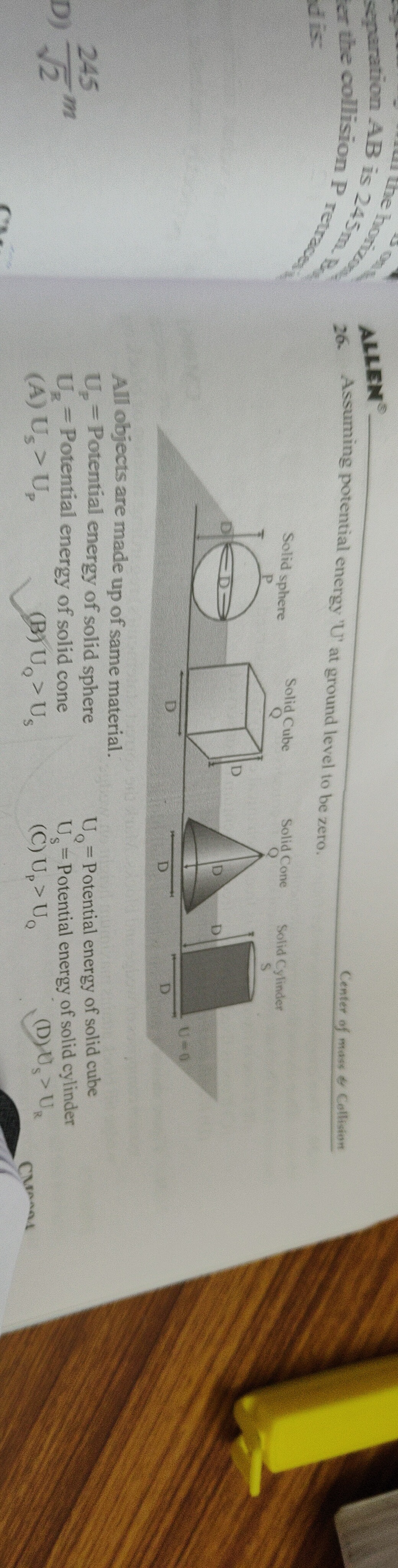
US>UPU_S > U_P

B

UQ>USU_Q > U_S

C

UP>UQU_P > U_Q

D

US>URU_S > U_R

Answer

A, B, D

Explanation

Solution

The potential energy of an object resting on the ground is given by U=MghCMU = Mgh_{CM}, where MM is the mass of the object, gg is the acceleration due to gravity, and hCMh_{CM} is the height of its center of mass from the ground. Since all objects are made of the same material, they have the same density, ρ\rho. The mass of an object is M=ρVM = \rho V, where VV is its volume. Therefore, the potential energy can be written as U=ρVghCMU = \rho V g h_{CM}.

Let's calculate the volume (VV) and the height of the center of mass (hCMh_{CM}) for each object, given that the characteristic dimension for all is D.

  1. Solid Sphere (P)

    • Diameter = D, so radius R=D/2R = D/2.
    • Volume VP=43πR3=43π(D2)3=4πD324=πD36V_P = \frac{4}{3}\pi R^3 = \frac{4}{3}\pi \left(\frac{D}{2}\right)^3 = \frac{4\pi D^3}{24} = \frac{\pi D^3}{6}.
    • Height of center of mass hCM,P=R=D2h_{CM,P} = R = \frac{D}{2}.
    • Potential energy UP=ρVPghCM,P=ρ(πD36)g(D2)=π12ρgD4U_P = \rho V_P g h_{CM,P} = \rho \left(\frac{\pi D^3}{6}\right) g \left(\frac{D}{2}\right) = \frac{\pi}{12} \rho g D^4.

  2. Solid Cube (Q)

    • Side length = D.
    • Volume VQ=D3V_Q = D^3.
    • Height of center of mass hCM,Q=D2h_{CM,Q} = \frac{D}{2}.
    • Potential energy UQ=ρVQghCM,Q=ρ(D3)g(D2)=12ρgD4U_Q = \rho V_Q g h_{CM,Q} = \rho (D^3) g \left(\frac{D}{2}\right) = \frac{1}{2} \rho g D^4.

  3. Solid Cone (R)

    • Base diameter = D, so base radius r=D/2r = D/2. Height H=DH = D.
    • Volume VR=13πr2H=13π(D2)2D=13πD24D=πD312V_R = \frac{1}{3}\pi r^2 H = \frac{1}{3}\pi \left(\frac{D}{2}\right)^2 D = \frac{1}{3}\pi \frac{D^2}{4} D = \frac{\pi D^3}{12}.
    • Height of center of mass hCM,R=H4=D4h_{CM,R} = \frac{H}{4} = \frac{D}{4} (from the base).
    • Potential energy UR=ρVRghCM,R=ρ(πD312)g(D4)=π48ρgD4U_R = \rho V_R g h_{CM,R} = \rho \left(\frac{\pi D^3}{12}\right) g \left(\frac{D}{4}\right) = \frac{\pi}{48} \rho g D^4.

  4. Solid Cylinder (S)

    • Base diameter = D, so base radius r=D/2r = D/2. Height H=DH = D.
    • Volume VS=πr2H=π(D2)2D=πD34V_S = \pi r^2 H = \pi \left(\frac{D}{2}\right)^2 D = \frac{\pi D^3}{4}.
    • Height of center of mass hCM,S=H2=D2h_{CM,S} = \frac{H}{2} = \frac{D}{2}.
    • Potential energy US=ρVSghCM,S=ρ(πD34)g(D2)=π8ρgD4U_S = \rho V_S g h_{CM,S} = \rho \left(\frac{\pi D^3}{4}\right) g \left(\frac{D}{2}\right) = \frac{\pi}{8} \rho g D^4.

Now, let's compare the numerical coefficients of ρgD4\rho g D^4 for each potential energy:

  • UP∝π12≈3.1415912≈0.2618U_P \propto \frac{\pi}{12} \approx \frac{3.14159}{12} \approx 0.2618
  • UQ∝12=0.5U_Q \propto \frac{1}{2} = 0.5
  • UR∝π48≈3.1415948≈0.06545U_R \propto \frac{\pi}{48} \approx \frac{3.14159}{48} \approx 0.06545
  • US∝π8≈3.141598≈0.3927U_S \propto \frac{\pi}{8} \approx \frac{3.14159}{8} \approx 0.3927

Comparing these values, we get the order: UR<UP<US<UQU_R < U_P < U_S < U_Q.

Let's check the given options: (A) US>UPU_S > U_P: Is 0.3927>0.26180.3927 > 0.2618? Yes, this is True. (B) UQ>USU_Q > U_S: Is 0.5>0.39270.5 > 0.3927? Yes, this is True. (C) UP>UQU_P > U_Q: Is 0.2618>0.50.2618 > 0.5? No, this is False. (D) US>URU_S > U_R: Is 0.3927>0.065450.3927 > 0.06545? Yes, this is True.

Therefore, options A, B, and D are correct.