Question

The line $x = \alpha$ meets the x-axis at A and the lines $ax^2 + 2hxy + by^2 = 0$ at B and C. If $AB = BC$, then

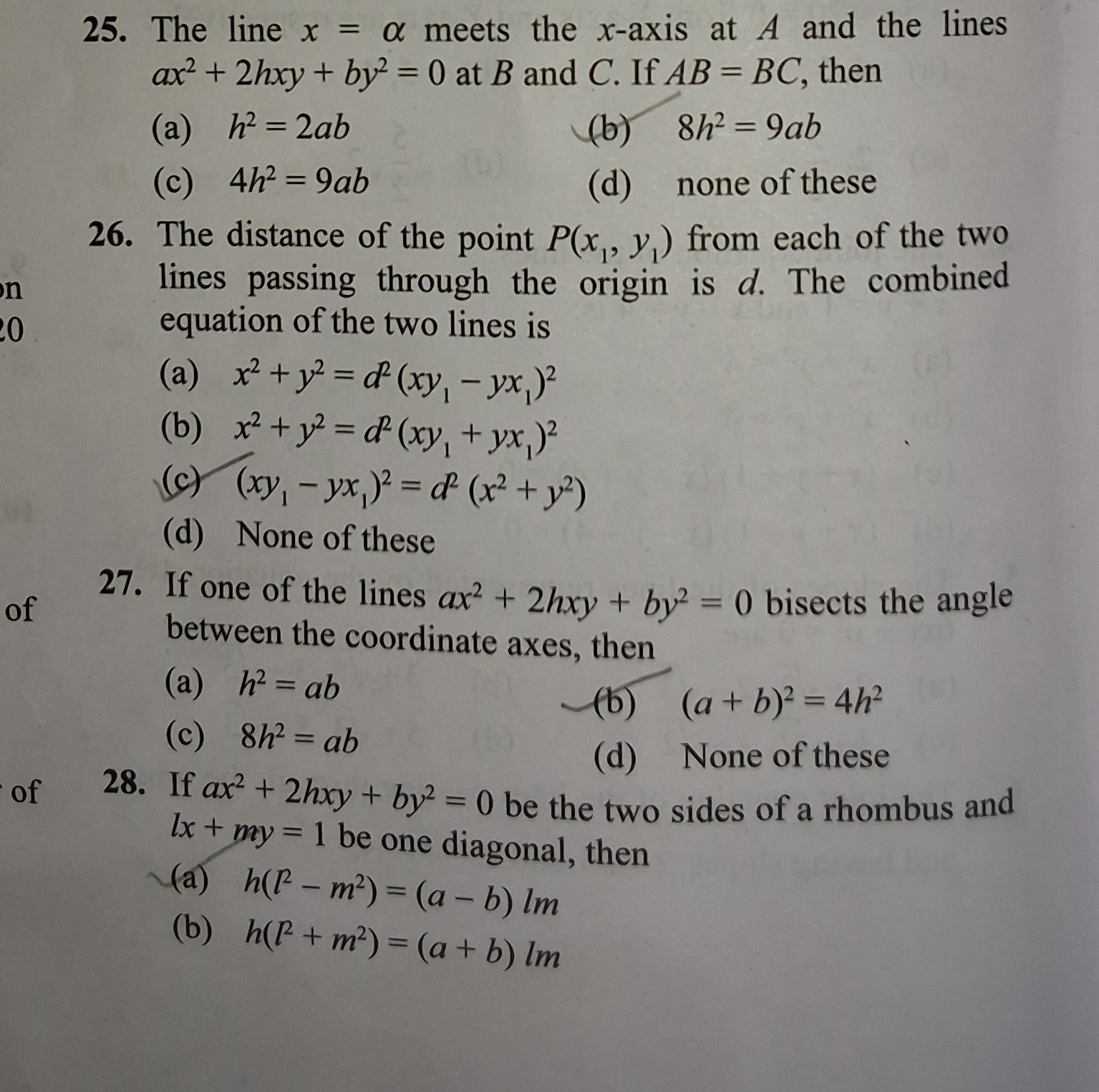
• A. $h^2 = 2ab$
• B. $8h^2 = 9ab$
• C. $4h^2 = 9ab$
• D. none of these

Answer 1

Answer: (B)

(b)

Answer 2

Let the combined equation of the two lines be $ax^2 + 2hxy + by^2 = 0$. These lines pass through the origin. The line $x = \alpha$ is a vertical line. Point A is the intersection of $x = \alpha$ and the x-axis ($y=0$). So, $A = (\alpha, 0)$.

To find the points B and C where the line $x = \alpha$ intersects the pair of lines $ax^2 + 2hxy + by^2 = 0$, substitute $x = \alpha$ into the equation: $a\alpha^2 + 2h\alpha y + by^2 = 0$ Rearranging this as a quadratic equation in $y$: $by^2 + (2h\alpha)y + a\alpha^2 = 0$

Let the roots of this quadratic equation be $y_1$ and $y_2$. These roots represent the y-coordinates of points B and C. So, $B = (\alpha, y_1)$ and $C = (\alpha, y_2)$.

The coordinates of A are $(\alpha, 0)$. The distance $AB = |y_1 - 0| = |y_1|$. The distance $BC = |y_2 - y_1|$.

The problem states that $AB = BC$. This implies $|y_1| = |y_2 - y_1|$. This gives two possibilities:

1. $y_1 = y_2 - y_1 \Rightarrow y_2 = 2y_1$
2. $y_1 = -(y_2 - y_1) \Rightarrow y_1 = -y_2 + y_1 \Rightarrow y_2 = 0$

If $y_2 = 0$, then one of the points (B or C) coincides with A. This means $C = (\alpha, 0)$. If $y_2 = 0$ is a root of $by^2 + (2h\alpha)y + a\alpha^2 = 0$, then substituting $y=0$ gives $a\alpha^2 = 0$. Since $\alpha$ is typically non-zero (otherwise the line $x=\alpha$ is $x=0$, which is one of the lines if $a=0$), we must have $a=0$. If $a=0$, the original equation of the pair of lines becomes $2hxy + by^2 = 0 \Rightarrow y(2hx + by) = 0$. The lines are $y=0$ and $2hx+by=0$. If $a=0$, then $8h^2 = 9ab$ becomes $8h^2 = 0$, which implies $h=0$. If $a=0$ and $h=0$, the equation is $by^2=0$, which means $y=0$. This is a single line, not a pair of distinct lines. Thus, $a \neq 0$, and therefore $y_2 \neq 0$.

So, we must have $y_2 = 2y_1$. From the quadratic equation $by^2 + (2h\alpha)y + a\alpha^2 = 0$: Sum of roots: $y_1 + y_2 = -\frac{2h\alpha}{b}$ Product of roots: $y_1 y_2 = \frac{a\alpha^2}{b}$

Substitute $y_2 = 2y_1$ into these equations: $y_1 + 2y_1 = -\frac{2h\alpha}{b} \Rightarrow 3y_1 = -\frac{2h\alpha}{b} \Rightarrow y_1 = -\frac{2h\alpha}{3b}$ $y_1 (2y_1) = \frac{a\alpha^2}{b} \Rightarrow 2y_1^2 = \frac{a\alpha^2}{b}$

Now, substitute the expression for $y_1$ from the first relation into the second relation: $2 \left(-\frac{2h\alpha}{3b}\right)^2 = \frac{a\alpha^2}{b}$ $2 \left(\frac{4h^2\alpha^2}{9b^2}\right) = \frac{a\alpha^2}{b}$ $\frac{8h^2\alpha^2}{9b^2} = \frac{a\alpha^2}{b}$

Since $\alpha \neq 0$ and $b \neq 0$, we can cancel $\alpha^2$ and one $b$: $\frac{8h^2}{9b} = a$ $8h^2 = 9ab$