Solveeit Logo
Login

Question

Question: Let \( y = \log_e(\frac{1-x^2}{1+x^2}), -1 < x < 1 \). Then at \( x = \frac{1}{2} \), the value of \...

Let y=log⁡e(1−x21+x2),−1<x<1y = \log_e(\frac{1-x^2}{1+x^2}), -1 < x < 1. Then at x=12x = \frac{1}{2}, the value of 225(y′′−y′)225(y'' - y') is equal to:

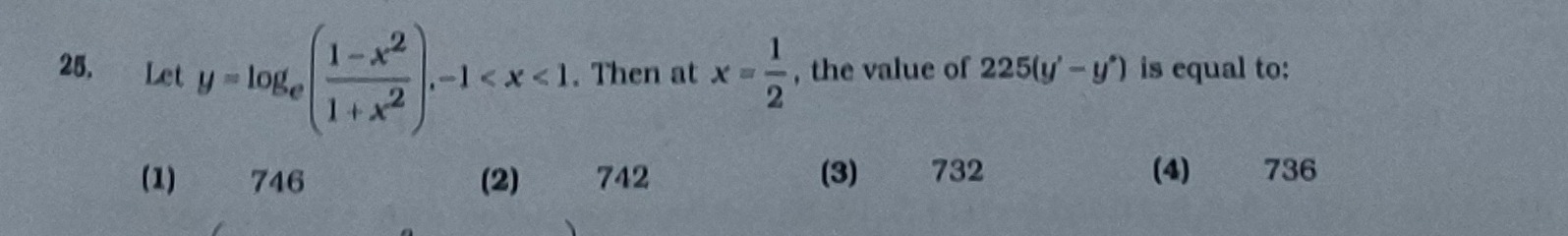
A

746

B

742

C

732

D

736

Answer

736

Explanation

Solution

The function is y=log⁡e(1−x21+x2)=log⁡e(1−x2)−log⁡e(1+x2)y = \log_e(\frac{1-x^2}{1+x^2}) = \log_e(1-x^2) - \log_e(1+x^2). The first derivative is y′=−4x1−x4y' = \frac{-4x}{1-x^4}. The second derivative is y′′=−4(1+3x4)(1−x4)2y'' = \frac{-4(1+3x^4)}{(1-x^4)^2}.

At x=12x = \frac{1}{2}: y′(12)=−4(12)1−(12)4=−21−116=−21516=−3215y'(\frac{1}{2}) = \frac{-4(\frac{1}{2})}{1 - (\frac{1}{2})^4} = \frac{-2}{1 - \frac{1}{16}} = \frac{-2}{\frac{15}{16}} = -\frac{32}{15}. y′′(12)=−4(1+3(12)4)(1−(12)4)2=−4(1+3(116))(1−116)2=−4(1916)(1516)2=−194225256=−194×256225=−1216225y''(\frac{1}{2}) = \frac{-4(1+3(\frac{1}{2})^4)}{(1-(\frac{1}{2})^4)^2} = \frac{-4(1+3(\frac{1}{16}))}{(1-\frac{1}{16})^2} = \frac{-4(\frac{19}{16})}{(\frac{15}{16})^2} = \frac{-\frac{19}{4}}{\frac{225}{256}} = -\frac{19}{4} \times \frac{256}{225} = -\frac{1216}{225}.

We need to calculate 225(y′′−y′)225(y'' - y'): y′′−y′=−1216225−(−3215)=−1216225+32×1515×15=−1216225+480225=−736225y'' - y' = -\frac{1216}{225} - (-\frac{32}{15}) = -\frac{1216}{225} + \frac{32 \times 15}{15 \times 15} = -\frac{1216}{225} + \frac{480}{225} = \frac{-736}{225}. So, 225(y′′−y′)=225×−736225=−736225(y'' - y') = 225 \times \frac{-736}{225} = -736.

Given that -736 is not an option, and assuming a typo in the question where it should be 225(y′−y′′)225(y' - y''), the value would be 225(y′−y′′)=225(−(−736225))=736225(y' - y'') = 225(-(-\frac{736}{225})) = 736.